Difference between revisions of "Wormholes"
| Line 59: | Line 59: | ||
<td>[[File:Sphere_and_great_circles.png|frameless]] | <td>[[File:Sphere_and_great_circles.png|frameless]] | ||
<td>[[File:Hyperbolic_surface_and_lines.png|frameless]] | <td>[[File:Hyperbolic_surface_and_lines.png|frameless]] | ||
<td>[[File:Cylinder_and_lines.png|frameless]] | |||
<tr> | <tr> | ||
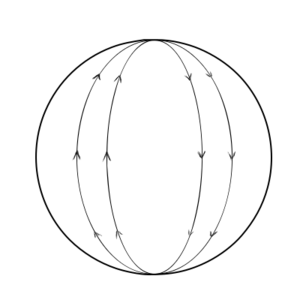
<td>Two great circles going around a sphere. Although initially parallel, they meet at two points. | <td width=400>Two great circles going around a sphere. Although initially parallel, they meet at two points. | ||
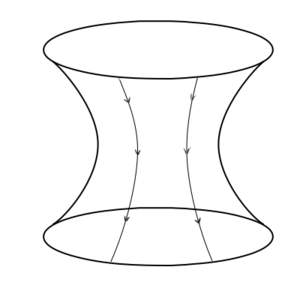
<td>Two initially parallel lines on a hyperbolic surface. As you get farther from the place where they are parallel, the lines diverge. | <td width=400>Two initially parallel lines on a hyperbolic surface. As you get farther from the place where they are parallel, the lines diverge. | ||
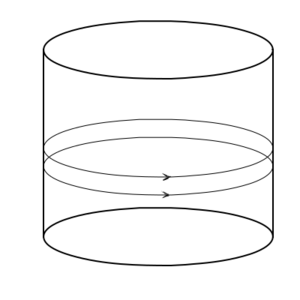
<td width=400>Lines that are initially parallel on a cylinder remain parallel everywhere. | |||
</table> | </table> | ||
On a sphere, parallel lines always end up converging. One example of a curved surface where parallel lines diverge is a hyperbolic surface. Like a sphere, a hyperbolic surface is a manifold | On a sphere, parallel lines always end up converging. One example of a curved surface where parallel lines diverge is a hyperbolic surface. Like a sphere, a hyperbolic surface is a manifold (at least, if you let it extend off to infinity). But it has the opposite sense of curvature. | ||
Now consider a cylinder. Again, an infinite cylinder is a manifold. A cylinder can be made by rolling up a plane. Like our construction of a loop, this can be done by simply taking and infinitely long rectangular section of a plane and saying that the two edges are actually the same (this is essentially what you do if you roll up a sheet of paper so that two of its parallel edges touch, and then pretend that they are merged together where they meet). This "rolling up" preserves distances, so any two parallel lines on the plane remain the same distance apart on the cylinder (think about that sheet of paper, and if you drew two parallel lines on it - they will stay the same distance apart when the paper is rolled up). A cylinder has <i>extrinsic</i> curvature – you can tell that it is curved when looking at it from three dimensions. But it has no <i>intrinsic</i> curvature – if you are confined to the surface of the cylinder it behaves locally as if it is flat. | |||
2D: planes, spheres, hyperbolic surfaces, cylinders, Mobeus strips, topological & curved toruses (& note on topology, multiply connected manifolds) | 2D: planes, spheres, hyperbolic surfaces, cylinders, Mobeus strips, topological & curved toruses (& note on topology, multiply connected manifolds) | ||
Revision as of 22:29, 1 November 2021
Wormholes are hypothetical structures in space-time allowed by the general theory of relativity. They provide short cuts through space-time that connect one region of space and time to another; potentially, these regions can be very distant from each other. The symmetries in space-time of our universe mean that wormholes move like physical objects, and acquire the conserved (or in some cases approximately conserved) quantities of things that go into them and lose those quantities of things that come out – properties like energy, mass, momentum, angular momentum, and electric charge.
What is a wormhole? The geometry of space-time and how to twist it into a pretzel
We're going to have to start out with some pretty heady stuff. Like the very nature of existence. And what is reality, anyway? Usually, space and time are so much an integral part of our existence that we don't even think of them at all. They simply form a backdrop on which all the interesting stuff plays out. But when we do think about them, we're so accustomed to living in a world where they exist and where distances are well defined and events can be uniquely identified based on where and when they happened (or are happening or will happen) that a lot of stuff seems so obvious that we don't stop to think about if it really has to be this way or if there are other possible ways of doing things.
A toy model
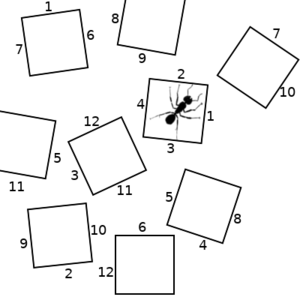
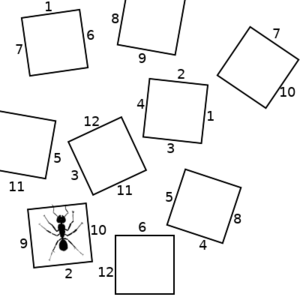
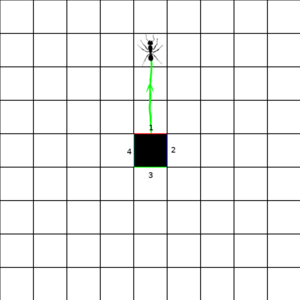
So lets consider a hypothetical scenario, where an ant can be in any of several states, represented by the squares in the pictures below. The ant can transition to any other state that has a numbered side with the same number as the state it is in. We will start on the left. If the ant chooses the "2" transition, we end up with the picture in the middle. If it then chooses the "10" transition, we end up with the state on the right.
| 
| 
|
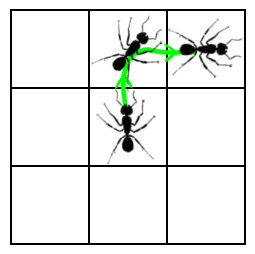
But now notice that the behavior of this system is exactly the same as if we re-arrange the states into a grid, as shown below on the left. The disconnected states now become a space; an expanse of coordinates on which the ant can exist. Now, the ant's transition between states can be described as a trajectory as shown in the right picture below.
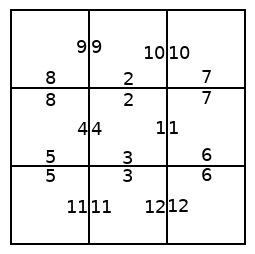
| 
|
This gives us an inkling of how something like space-time might end up being assembled from individual events. But what if we don't have things match up into quite such a perfect grid? We ll take our space elements and tile them into an infinite grid. Two sections of the grid are shown below. But now we remove two of those space-tiles, and we connect the edges adjacent to the removed tiles with a corresponding edge of the other removed tile (although, as shown in the figure, we don't have to keep the same orientation). Now the ant, entering side 1 (which we have color-coded red for convenience) comes out of side 1 of the other missing square. This is perhaps the most basic wormhole.
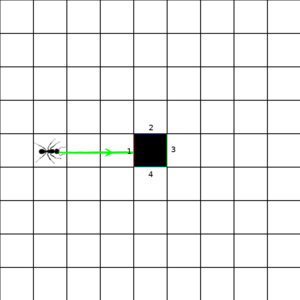
| 
|
Of course, this simple assembly only stitches together a space. But the world we live in is one of space-time. As the ant transitions from one square to another, it is also transitioning further ahead in time. But when the ant passes through the wormhole, while it locally experiences no discontinuity that wormhole might connect to a different time as well as a different region of space. So the ant might emerge far in the past or future of when it stepped through.
Manifolds and coordinate patches
The toy model used above hopefully prepares you for some of the ideas to follow - one of how we can piece together a complete space and time by connecting together different pieces. But before we go further, lets define an important term: a manifold is a "shape" of a given number of dimensions where, if you zoom in close enough, you can always get to a scale where it looks like the shape is flat. We'll use this definition to help us describe how we can put space and time together to get a wormhole. But first, let's look at a few illustrative examples.
One dimension
The simplest one dimensional shape is a line. And a line is everywhere flat. So a line is a one dimensional manifold.
A one dimensional shape might seem to be a wiggly path if inscribed in two or more dimensions, but it has no intrinsic curvature. That is, if everything about your world is confined to that path, you can't tell that it is curved – all you can do is measure the distance you go along the path. This greatly limits the kinds of shapes that we can consider. So any curved path of infinite extent looks from the inside like a line, and so any infinite length path is also a manifold.
But there's another class of one dimensional shapes that are manifolds – loops. A loop is a path of fine length that connects back with itself. You can make one by drawing a closed curve in a higher dimensional space. Or you can take a straight line but then say that a given point here maps on to another point there, and all the points between here and there form a loop. When you are marching along the line starting at there and you reach here you are also at there, so if you go further you just end up back where you were. This last bit may seem like a pointless bit of pedantry that just confuses a simple problem, but it will be a very useful way of looking at things as we go on.
One thing that is not a manifold is a ray. A ray starts at a point, but then goes off to infinity in a given direction. A ray almost meets the definition of a manifold, except at the place that it starts. It's not flat there – the 1D space just ends. So it is not a manifold. For the same reason, a line segment that starts at a point and ends at another point is not a manifold.
Two dimensions
The simplest two dimensional manifold is a plane. A plane is everywhere flat, and extends off to infinity. A small region around any point on a plane (naturally) locally looks like a plane, so it meets our definition of a manifold.
But in two dimensions, we can have something that we don't have in one dimension – intrinsic curvature. Consider a sphere. If you get close enough to the sphere, it will look like you are on a plane; we live on a world that is (approximately) spherical (if you neglect mountains and ocean basins and all that other stuff), but when you stand up and look around you it mostly looks flat. So a sphere is a manifold. But take a line on the surface of your sphere. Extend it out along the surface, drawing it as straight as possible. Eventually, it will go all the way around the sphere, dividing it in two, and meet itself. This path is called a great circle. The Earth's equator is (approximately) a great circle, as are the lines of longitude (but not lines of latitude, because they do not divide the Earth into two equal-sized halves).
In flat space, two lines that are initially parallel remain parallel, always remaining the same distance apart. But in a curved space, initially parallel lines do not remain the same distance apart. On a sphere, for example, any two great circles will intersect at two points. A sphere this has intrinsic curvature.
On a sphere, parallel lines always end up converging. One example of a curved surface where parallel lines diverge is a hyperbolic surface. Like a sphere, a hyperbolic surface is a manifold (at least, if you let it extend off to infinity). But it has the opposite sense of curvature.
Now consider a cylinder. Again, an infinite cylinder is a manifold. A cylinder can be made by rolling up a plane. Like our construction of a loop, this can be done by simply taking and infinitely long rectangular section of a plane and saying that the two edges are actually the same (this is essentially what you do if you roll up a sheet of paper so that two of its parallel edges touch, and then pretend that they are merged together where they meet). This "rolling up" preserves distances, so any two parallel lines on the plane remain the same distance apart on the cylinder (think about that sheet of paper, and if you drew two parallel lines on it - they will stay the same distance apart when the paper is rolled up). A cylinder has extrinsic curvature – you can tell that it is curved when looking at it from three dimensions. But it has no intrinsic curvature – if you are confined to the surface of the cylinder it behaves locally as if it is flat.
2D: planes, spheres, hyperbolic surfaces, cylinders, Mobeus strips, topological & curved toruses (& note on topology, multiply connected manifolds)
3D: spaces
3+1D: space-time!
Common kinds of wormholes
Early work, Einstein-Rosen bridges, and their issues.
Spherically symmetric wormholes
Morris-Thorne wormholes
Thin shell wormholes
Including polyhedral wormholes.
Non-orientable wormholes
Fields and conserved properties
Wormhole dynamics
Does gravity go through a wormhole?
Can negative mass wormholes exist?
(also, discuss zero mass case)
Wormholes and time travel
Practical implications
Can I put it on a planet? (Mass, tidal forces, radiant flash from collapse accidents, "gravity" limit only consistent as tidal forces)
Spacecraft radiators -> wormhole spacecraft.
Credit
Author: Luke Campbell