Wormholes

🔨	Notice:
	This page is under construction.

Wormholes are hypothetical structures in space-time allowed by the general theory of relativity. They provide short cuts through space-time that connect one region of space and time to another; potentially, these regions can be very distant from each other. The symmetries in space-time of our universe mean that wormholes move like physical objects, and acquire the conserved (or in some cases approximately conserved) quantities of things that go into them and lose those quantities of things that come out – properties like energy, mass, momentum, angular momentum, and electric charge.

What is a wormhole? The geometry of space-time and how to twist it into a pretzel

We're going to have to start out with some pretty heady stuff. Like the very nature of existence. And what is reality, anyway? Usually, space and time are so much an integral part of our existence that we don't even think of them at all. They simply form a backdrop on which all the interesting stuff plays out. But when we do think about them, we're so accustomed to living in a world where they exist and where distances are well defined and events can be uniquely identified based on where and when they happened (or are happening or will happen) that a lot of stuff seems so obvious that we don't stop to think about if it really has to be this way or if there are other possible ways of doing things.

A toy model

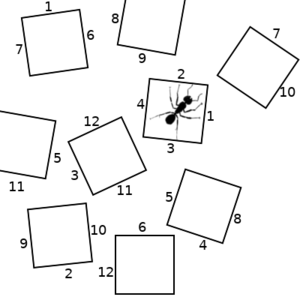
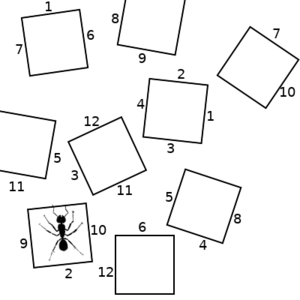
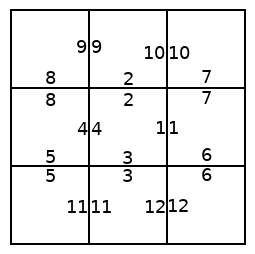
So lets consider a hypothetical scenario, where an ant can be in any of several states, represented by the squares in the pictures below. The ant can transition to any other state that has a numbered side with the same number as the state it is in. We will start on the left. If the ant chooses the "2" transition, we end up with the picture in the middle. If it then chooses the "10" transition, we end up with the state on the right.

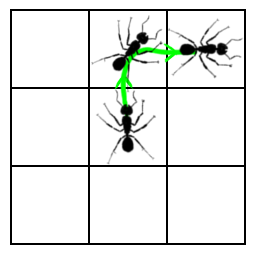
But now notice that the behavior of this system is exactly the same as if we re-arrange the states into a grid, as shown below on the left. The disconnected states now become a space; an expanse of coordinates on which the ant can exist. Now, the ant's transition between states can be described as a trajectory as shown in the right picture below.

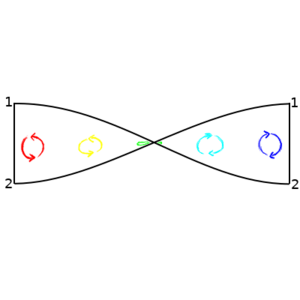
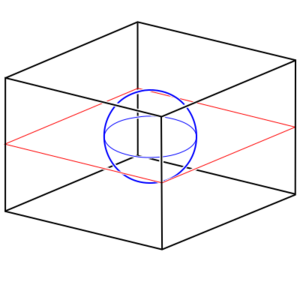
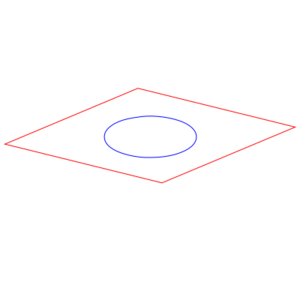
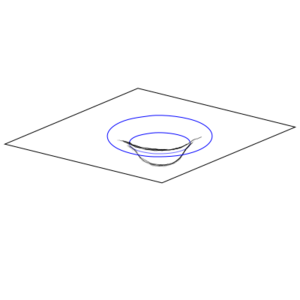
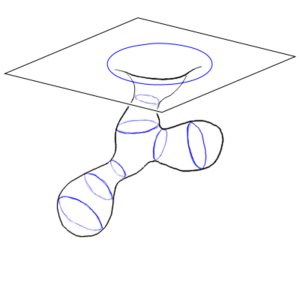
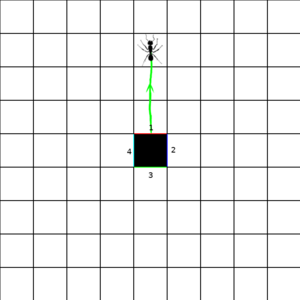
This gives us an inkling of how something like space-time might end up being assembled from individual events. But what if we don't have things match up into quite such a perfect grid? We ll take our space elements and tile them into an infinite grid. Two sections of the grid are shown below. But now we remove two of those space-tiles, and we connect the edges adjacent to the removed tiles with a corresponding edge of the other removed tile (although, as shown in the figure, we don't have to keep the same orientation). Now the ant, entering side 1 (which we have color-coded red for convenience) comes out of side 1 of the other missing square. This is perhaps the most basic wormhole.

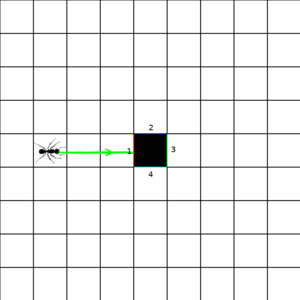
Of course, this simple assembly only stitches together a space. But the world we live in is one of space-time. As the ant transitions from one square to another, it is also transitioning further ahead in time. But when the ant passes through the wormhole, while it locally experiences no discontinuity that wormhole might connect to a different time as well as a different region of space. So the ant might emerge far in the past or future of when it stepped through.

Manifolds and coordinate patches

The toy model used above hopefully prepares you for some of the ideas to follow - one of how we can piece together a complete space and time by connecting together different pieces. But before we go further, lets define an important term: a manifold is a "shape" of a given number of dimensions where, if you zoom in close enough, you can always get to a scale where it looks like the shape is flat. We'll use this definition to help us describe how we can put space and time together to get a wormhole. But first, let's look at a few illustrative examples.

One dimension

The simplest one dimensional shape is a line. And a line is everywhere flat. So a line is a one dimensional manifold.

A one dimensional shape might seem to be a wiggly path if inscribed in two or more dimensions, but it has no intrinsic curvature. That is, if everything about your world is confined to that path, you can't tell that it is curved – all you can do is measure the distance you go along the path. This greatly limits the kinds of shapes that we can consider. So any curved path of infinite extent looks from the inside like a line, and so any infinite length path is also a manifold.

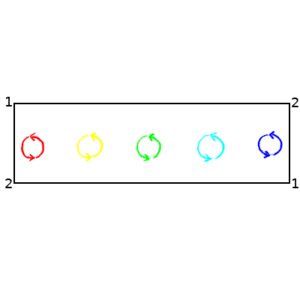
But there's another class of one dimensional shapes that are manifolds – loops. A loop is a path of fine length that connects back with itself. You can make one by drawing a closed curve in a higher dimensional space. Or you can take a straight line but then say that a given point here maps on to another point there, and all the points between here and there form a loop. When you are marching along the line starting at there and you reach here you are also at there, so if you go further you just end up back where you were. This last bit may seem like a pointless bit of pedantry that just confuses a simple problem, but it will be a very useful way of looking at things as we go on.

Two dimensions

The simplest two dimensional manifold is a plane. A plane is everywhere flat, and extends off to infinity. A small region around any point on a plane (naturally) locally looks like a plane, so it meets our definition of a manifold.

Curved manifolds

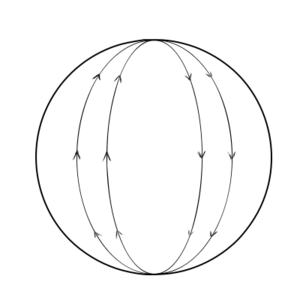
But in two dimensions, we can have something that we don't have in one dimension – intrinsic curvature. Consider a sphere. If you get close enough to the sphere, it will look like you are on a plane; we live on a world that is (approximately) spherical (if you neglect mountains and ocean basins and all that other stuff), but when you stand up and look around you it mostly looks flat. So a sphere is a manifold. But take a line on the surface of your sphere. Extend it out along the surface, drawing it as straight as possible. Eventually, it will go all the way around the sphere, dividing it in two, and meet itself. This path is called a great circle. The Earth's equator is (approximately) a great circle, as are the lines of longitude (but not lines of latitude, because they do not divide the Earth into two equal-sized halves).

In flat space, two lines that are initially parallel remain parallel, always remaining the same distance apart. But in a curved space, initially parallel lines do not remain the same distance apart. On a sphere, for example, any two great circles will intersect at two points. A sphere thus has intrinsic curvature.

Two great circles going around a sphere. Although initially parallel, they meet at two points.	Two initially parallel lines on a hyperbolic surface. As you get farther from the place where they are parallel, the lines diverge.	Lines that are initially parallel on a cylinder remain parallel everywhere.

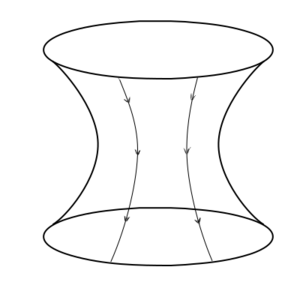
On a sphere, parallel lines always end up converging. One example of a curved surface where parallel lines diverge is a hyperbolic surface. Like a sphere, a hyperbolic surface is a manifold. But it has the opposite sense of curvature.

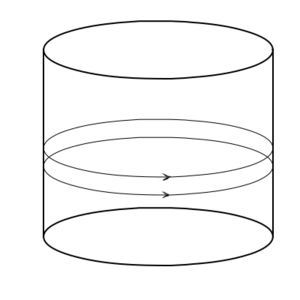
Now consider a cylinder. Again, a cylinder is a manifold. A cylinder can be made by rolling up a plane. Like our construction of a loop, this can be done by simply taking a long rectangular section of a plane and saying that two of the parallel edges are actually the same (this is essentially what you do if you roll up a sheet of paper so that two of its parallel edges touch, and then pretend that they are merged together where they meet). This "rolling up" preserves distances, so any two parallel lines on the plane remain the same distance apart on the cylinder (think about that sheet of paper, and if you drew two parallel lines on it - they will stay the same distance apart when the paper is rolled up). A cylinder has extrinsic curvature – you can tell that it is curved when looking at it from three dimensions. But it has no intrinsic curvature – if you are confined to the surface of the cylinder it behaves locally as if it is flat.

A manifold that is flat obeys all the rules of Euclidean geometry (although you'll need to go to the three dimensional case for dealing with volumes), and the standard Cartesian coordinate system (representing position by two orthogonal coordinates, commonly called $x$ and $y$) can be used to specify any point. A manifold that is not flat violates Euclid's fifth postulate; the geometry of the manifold will be non-Euclidean (somewhere, H. P. Lovecraft is quietly having a mental breakdown). It cannot be represented by Cartesian coordinates, but different sets of coordinates – or perhaps patches of multiple coordinate systems that apply in different places – can be defined instead to locate points.

Topology: simply and multiply connected manifolds

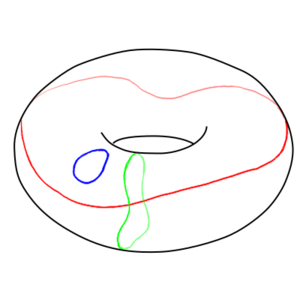
If you take a plane or a sphere, any closed loop on the manifold can be shrunk in a continuous manner until it vanishes. This is called simply connected. But not all manifolds are simply connected. Those which are not simply connected are called multiply connected. In fact, all wormhole manifolds are multiply connected. The most basic multiply connected manifold is a torus, like a bagel or doughnut or bicycle inner tube. While there are closed loops on a torus that can be shrunk to a point and made to vanish, those that go all the way around the torus tube cannot – they'll get caught up circling the tube. Likewise, loops that go all the way along the tube will get caught up on the central hole if they are shrunk and again cannot be made to go to a point.

The three classes of loops on a torus. On the left is a standard geometrical torus; on the right is a topological torus that is flat but has opposite edges identified so that they are connected. The blue loop doesn't go around the torus, it can be continuously deformed to shrink to a point and vanish. The red line goes around the torus the long way. If you shrink it, it will get caught up going around the hole in the middle and get stuck there; it cannot be continuously deformed to make it any smaller. The green line loops around the torus from the outside to the inside and back. Again, if you shrink it the line gets caught up circling the torus tube and can't be made any smaller.

And this brings us to another interesting kind of manifold. You can get a manifold that is flat but has the topology of a torus. You can do this by taking a rectangle and saying that the opposite sides are actually the same. This gives you the effect of a "wrap-around screen" like on that old arcade game Asteroids – if you go off the edge on one side, you just come back on the opposite side at the same height. in physics, this is known as "periodic boundary conditions". Closed loops that go all the way around one way or the other cannot be shrunk to a point. But this kind of surface cannot be embedded in three-dimensional space! We might have grown used to surfaces that we can envision existing in the space we live in, but there are manifolds, even fairly simple two-dimensional manifolds, that cannot be embedded in higher-dimensional spaces like that. Remember this when we get to actual wormholes.

You can have multiply connected manifolds that are not toruses, even though they might have the same topology; any manifold with one or more "loops" or "handles" is multiply connected.

Non-orientable manifolds

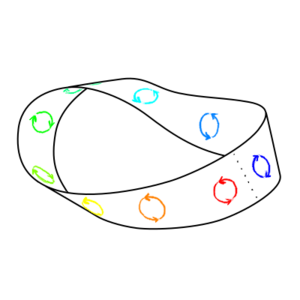
And there is one other interesting kind of manifold that is relevant to wormholes – manifolds that are non-orientable. An orientable manifold is one where you can define a consistent sense of clockwise and counter-clockwise everywhere on the manifold. If you start with a clock spinning clockwise, or a right-handed glove, or a copy of Lewis Carrol's "Through the Looking-Glass, and What Alice Found There", you can move it anywhere on the surface and if it meets back up with itself it will still be spinning clockwise, or right handed, or normally readable. But in a non-orientable surface, there are ways you can move the object so that when you get it back to where it originally was the clock is spinning counter-clockwise, or the glove is left-handed, or the book is written in mirror writing. The simplest example of such a surface is a Mobius strip. As shown below, if you move an oriented circle around the strip, it comes back with the opposite orientation.

A Mobius strip … a strip of surface with a twist so the edges where it connects meet up "the wrong way around". On the right is a 2D strip where you connect along the short edge matching the 1's together and the 2's together. The center shows the same strip with a twist in it so you can line the edges up the way you are supposed to, demonstrating how the twist reverses the orientation of the spinning circles. An embedded image in 3D space with the edges connected together is shown on the left. You cannot define a consistent orientation to this surface – starting at the red counter-clockwise circle, if you move the circle continuously along the surface when you get back where you started you will find it is going clockwise!

Three dimensions

The most basic three-dimensional manifold is a flat space. This is, well, just a normal space. You can go off in any combination of three independent directions (left-right, up-down, front-back), and because it is flat, initially parallel lines stay parallel. It all behaves much as you would expect three dimensional spaces to behave.

But you can get variations on this. They are harder to visualize than two-dimensional cases, because we don't have the brainspace for processing curved spaces inside of a four-dimensional hyperspace. But you can do things like identifying two planes to be the same, such that if you go far enough in one direction you can end back up where you started again (akin to a cylinder), or make them curved such that distances are distorted and lines don't remain parallel and maybe you can put larger things inside of smaller surfaces. There are 3D equivalents of spherical and hyperbolic surfaces (called, naturally enough, spherical and hyperbolic spaces). There are even non-orientable spaces.

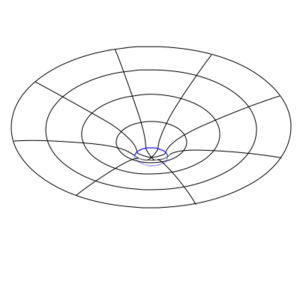
One way of trying to envision a curved space, and to gain some intuition about them, is to take a two-dimensional slice of that curved space and embed that in a flat three-dimensional space. This is called an embedding diagram. Remember that this is a reduced representation that throws away a lot of the information (unless there are special symmetries you can exploit) and is not actually the thing being described.

A space with an embedded plane. We show a sphere in this space, with the plane bisecting the sphere.	Just the embedded plane. Note how in a spherically symmetric manifold (like this space), a circle on the embedding diagram represents a complete 2-dimensional spherical surface.	An embedding diagram of a "dimpled" space. Just as before, the closed circles represent closed spherical surfaces. It is just that in this case, the distance between two concentric spheres of radius $R_{1}$ and $R_{2}$ is longer than the usual $R_{1}-R_{2}$ because of the spatial curvature, as shown by the increasing distance along the dimple's surface.	An embedding diagram of an extremely curved section of space. In this example, there are several places where we have a bigger sphere inside of a smaller one! Curved space is weird like that.

Remember that not every manifold can be embedded, so not every curved space can be represented by an embedding diagram. But you can take patches of the curved space and show them by embedding diagrams, and then describe how these patches stitch together to create a contiguous surface.

Space-time: three space dimensions and one time dimension

This is the world we live in. So this is the class of manifolds that we really need to use when making a wormhole. Sometimes it's abbreviated as 3+1D as opposed to 1D, 2D, 3D, etc.).

The basic, infinite, flat space-time manifold is often called Minkowski space. I know, it's a big word using scary foreign-sounding names. But all it means is that its a 3+1D manifold that goes on forever and is flat. In flat space-time, everything obeys the rules of special relativity. Which means it really doesn't work when masses become significant enough to make gravity.

Our best model of how gravity works is general relativity. In this theory, the curvature of space-time is created by mass. At least, that's what they always say in the over-simplified pop-sci summaries of general relativity. Actually, space-time curvature is created by all the components of the stress-energy tensor. It's just that in almost all cases, mass is the most significant part of this. But momentum, stresses, pressures, and shear forces all have contributions as well. In general relativity, physical objects move along the straightest possible lines in this curved space-time. The way the curvature causes the lines to bend and converge is what leads to the appearance of gravity as a force if the curvature is sufficiently weak.

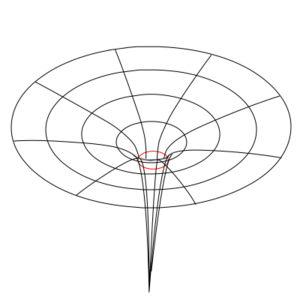
The most basic curved space-time manifold is the Schwarzschild geometry, which is what you get when you have an uncharged, non-spinning spherical mass doing its distortion thing on space-time. The Schwarzschild geometry is static meaning it does not change in time, and is spherically symmetric, meaning that it has a definite center and it doesn't matter which direction you are relative to that center – it is independent of angle. If the mass becomes dense enough, space-time gets so distorted that an event horizon forms. Nothing that goes into the event horizon can ever come back out, and the inevitability of the geometry crushes the mass down to an infinitely dense point at the center called a singularity. Nothing on the inside of the horizon can ever escape. It forms a black hole, that forever traps any light or matter that enters it. For masses that don't exceed this critical density, the gravitational distortion outside of the object is the same as for a black hole of equal mass, but there is no event horizon. The object can still be seen and interacted with.

An embedding diagram of the Schwarzschild geometry of a dense, massive star. The physical extent of the star is shown in blue.	An embedding diagram of the Schwarzschild geometry of a black hole of the same mass as the star to the right. The event horizon is shown in red.

There is one distinction between space-time manifolds that will become important later. Some manifolds have an isolated region of high curvature (corresponding to a concentration of mass, or at least of stress-energy) but as you go farther away from the strongly curved region the space-time becomes increasingly flat. If you can always go out far enough away from a curved region that space-time becomes flatter that whatever flatness criterion you choose, no matter what direction you choose to leave the curved region, the manifold is called asymptotically flat. For our purposes, if you can go far enough away that the Newtonian approximation to general relativity is accurate, and gravity can be described as a force rather than requiring a geometric description, then the geometry can be considered asymptotically flat. Both the Schwarzschild and the Minkowski geometries are asymptotically flat. Spherical or hyperbolic geometries are not asymptotically flat. Planets, stars, galaxies, neutron stars, black holes, and galactic clusters are all approximately asymptotically flat; but the universe as a whole is not. As long as we confine our attention to merely galactic clusters, we can make the approximation of asymptotic flatness.

Making a wormhole

Now that we have covered some of the introductory material, we can get down to the main course. To make a wormhole, take two regions of space-time, usually far apart and usually asymptotically flat (although neither of these is strictly required) and connect them together. That's it. You're done. Sounds easy, doesn't it?

Common kinds of wormholes

Spherically symmetric wormholes

General relativity involves a lot of non-trivial math. You need to deal with four-dimensional curvature tensors with up to 20 independent components, and figure out how they relate to a given distribution of matter, fields, energy, stresses, and material flows. If you can reduce the number of dimensions you need to keep track of, it can simplify things a lot. One way of doing this is assuming your space-time geometry does not change with time (it is static), and looks the same in all directions when viewed from a central point (it is spherically symmetric). This makes things a lot easier to analyze.

Astute readers will have noticed that these conditions are satisfied by the Schwarzschild geometry. In fact, if you play around with the Schwarzschild geometry enough, you will find that you can even get a wormhole-like solution. At the event horizon, you can connect your black hole solution to a time-reversed structure called a white hole. This is called an Einstein-Rosen bridge. Unfortunately, it has some issues. For one, it can't form naturally from infalling matter creating a black hole. For another, going through an Einstein-Rosen bridge involves passing through an event horizon, so the trip is necessarily one way. And finally, you can show that even the smallest amount of matter or radiation falling into the Einstein-Rosen bridge leads to it collapsing before the matter or radiation can pass through, trapping it inside the black hole. So this is not looking particularly useful.

So what are we going to do? Well, the Einstein-Rosen bridge, like a lot of early work in general relativity, was made by assuming a distribution of stress-energy (in this case, matter) that was assumed to be physically plausible, and finding out what the resulting geometry would be. But we want a wormhole, dangit! So what happens if we just demand a static tunnel connecting two asymptotically flat regions of space-time? If you do this, you get a Morris-Thorne wormhole. You still have the relation between stress-energy and geometry, but now it is your assumed geometry dictating the stress-energy rather than the other way around.

One issue when doing this is that you end up with regions where the energy density is negative. More strictly, there are regions where the tension is higher than the energy density – which necessarily means that in some frames of reference observers will measure a negative energy density there. A lot of physicists used to be reflexively dismissive of negative energy densities. After all, they can't really exist; all energy in the real world is positive.

Except that it is not. There are certain odd cases that allow for negative energy densities. One of these is the Casimir vacuum. A conducting boundary cannot support an electric field parallel to that boundary (if there was such a field, charge would flow under the force of the field until the parallel component of the field is screened out). So if you have two parallel conductive plates, the only electromagnetic waves that you can get between them require their fields to vanish at the plates. This restricts the number of ways the electromagnetic field can vibrate, called modes. In quantum mechanics, merely the potential for a vibration is associated with a certain energy (called zero point energy) even if no quanta of vibration are actually present. By making these modes impossible, they cannot contribute their zero point energy to the region between the plates. This lowers the total energy of the space between the plates compared to the region outside the plates (or with the plates absent). Because the energy of empty space is zero, this means that the region between these Casimir plates has negative energy. The Casimir effect has been measured in the laboratory. It is fairly weak, but it is present. In fact, not long after traversable wormholes were first described, one proposal showed how to hold open the wormhole using the Casimir effect

Thin shell wormholes

Including polyhedral wormholes.

Reducing or eliminating ANEC violating stuff

Fermionic wormholes

"Traversable Wormholes with Aribtrarily Small Energy Condition Violations"

Toroidal wormholes

"On wormholes with arbitrarily small quantities of exotic matter"

Fields and conserved properties

Can negative mass wormholes exist?

(also, discuss zero mass case)

Practical implications

Can I make one that goes where I want to go? (short answer: no. You have to make both ends in the same place and then move it there. But ER = EPR offers some possibilities)

How do I move it?

Can I put it on a planet? (Mass, tidal forces, radiant flash from collapse accidents, "gravity" limit only consistent as tidal forces)

Spacecraft radiators -> wormhole spacecraft.

Tiny wormholes: communications, energy.

Causality denial, causality attacks.

Credit

Author: Luke Campbell