Attenuation
A beam of radiant energy going through the air will have some of that energy absorbed, or removed from the beam by making the radiation no longer exist, and some of it scattered, or removed from the beam by making the radiation go in a different direction. Together, these make up the attenuation of the radiant energy, or removal of energy from the beam.
The Beer-Lambert law
Numerically, the attenuation is represented by an attenuation length R0, which is the distance at which the intensity of the light (or beam power, or pulse energy) has been reduced to approximately 37% of its original value. If you start off with an intensity I0, or a power P0, or an energy E0, then the intensity I, power P, and energy E after a given range R will be
| I | = | I0 exp[-R/R0] |
| P | = | P0 exp[-R/R0] |
| E | = | E0 exp[-R/R0]. |
This is called the Beer-Lambert law. [1] [2] [3]
If you have more than one physical phenomenon contributing to attenuation (for example, absorption and scattering, or absorption off of oxygen and absorption off of nitrogen), the inverses of the attenuation lengths of each phenomena add together. In particular, if you have scattering with a characteristic scattering length Rs and absorption with a characteristic absorption length Ra, then
1 / R0 = 1 / Ra + 1 / Rs.
Absorption
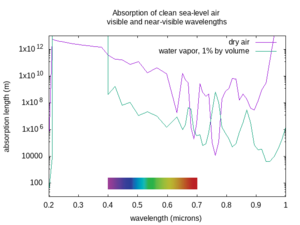
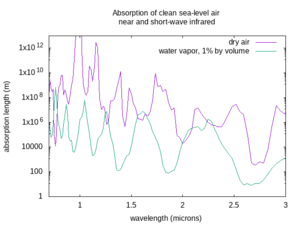
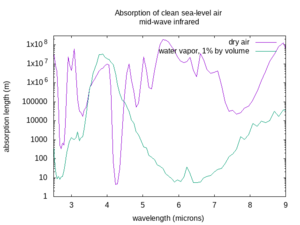
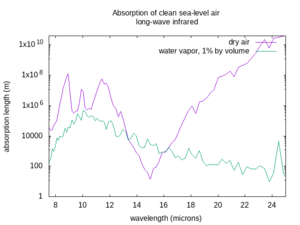
The first thing to worry about with the air is that it can absorb light. It can absorb some colors of light better than others. Clear air with an Earth-like composition is very transparent to visible light, as well as to nearby invisible colors like near and short-wave infrared, or ultraviolet A, B, and C. But some wavelengths of mid-wave, long-wave, and far infrared are absorbed, and some get through depending on the exact wavelength. Also, any light with a shorter wavelength than ultraviolet-C gets rapidly absorbed by air, hence the name “vacuum ultraviolet” for frequencies higher than UV-C, as they can only propagate in vacuum. If your laser works at a frequency that is absorbed by the air, it will not be very useful in that environment.
Even if the absorption length is much longer than the distance to the target, it can still have significant effects on laser performance because absorption is what drives thermal blooming.
The absorption length varies a lot depending on the wavelength of the beam, the weather, and the atmospheric conditions. The figures below show the absorption lengths for clean air at sea level without aerosols, for both dry air and only the absorption of water vapor at 1% concentration by volume in that air[4] (corresponding to approximately 60% relative humidity at 15 °C. In humid tropical climates, the water vapor concentration may be as high as 5% by volume; in dry or arctic conditions it may be less than 0.1% by volume). Divide the water vapor attenuation length by the percent concentration by volume of water vapor, and find the total absorption length by taking the inverse of the sum of the inverse absorption lengths for dry air and the water vapor, as described above. Non-Earthlike atmospheres may have very different clean atmosphere absorption.
Scatter

The next thing to worry about is scatter. Rather than simply making the light in your beam go away, scatter is what makes the light go in a different direction. Particulates or aerosols in the air are good at scattering light. This is why we can’t see through fog or clouds. But even perfectly clean air will scatter light to some extent. The electric field in the light will make the electrons in air molecules slosh back and forth at the light’s frequency. And these electrons then act like antennas to radiate light away in different directions (while simultaneously taking that energy away from the beam). This is called Rayleigh scattering, and it is more effective for higher frequency light than lower frequency light. This is why, for example, the sky looks blue - more high frequency blue light from the sun is being scattered into our eyes than lower frequency light of other colors. The Rayleigh scattering length for clean sea level air is [5]
RRayleigh = 948 km [ λ / (1 μm)]4
for wavelength λ.
Note that scatter makes it so you can see the laser beam. Even a 1 watt blue laser shows up clearly in clean air from its Rayleigh scattering. A very powerful visible light laser like you would use for a weapon will give an obvious trace through the air.
Estimating attenuation due to aerosols
The attenuation length of aerosols such as clouds, fog, smoke, smog, dust, lint, or pollen can be roughly estimated by figuring out how far away you can see before the things you are looking at appear somewhat hazy or washed out. Usually, this attenuation will mostly be scatter, but smoke, dust, pollen, or lint may introduce a substantial amount of absorption as well.
Different atmospheres
The attenuation of atmospheres of greatly different composition than the Earth – especially in the infrared – goes well beyond the scope of this document. You can make a quick estimate, however, by dividing the attenuation length without aerosols by the planet's atmospheric pressure relative to Earth and then figure the effect of aerosols separately. This method is more accurate the closer the planet's atmospheric composition is to Earth. Unless the atmosphere contains chlorine, fluorine, nitrogen dioxide, far more ozone than Earth's air, or approaching an atmospheric pressure or more of methane, the air will be nearly transparent to visible light; although the scattering may vary by a factor of two or so depending on the polarizabilities of the air molecules.
This can also be used to estimate the attenuation of air on Earth at different altitudes.
Shooting through the atmosphere
If you are in orbit around a planet and trying to shoot at ground targets, or if you are on the ground trying to shoot at spacecraft in orbit, it helps to be able to estimate the effective thickness of the air. To go from Earth to space or vice versa, you need to shoot through an effective distance of 8.5 km of air at the density of the shooter or target in the air. This distance is called the scale height. For other planets, you can use
scale height = 8.5 km × [ T / (288.15 K) ] × [ (9.80 m/s²) / g] × [ (28.96 g/mole) / W]
where T is the average temperature, g is the acceleration due to gravity, and W is the average molecular weight of the gases in the air. If you are shooting through the atmosphere at an angle, the distance of all that atmospheric junk you need to go through can be approximated as the scale height divided by the cosine of the angle you are shooting at. The amount of air you have to get through along your beam path is called the air mass, and if you follow the link you will find more accurate methods of approximating it if you need to.
Credit
Author: Luke Campbell
References
- ↑ https://archive.org/details/UFIE003101_TO0324_PNI-2703_000000 Bouguer, Pierre (1729). Essai d'optique sur la gradation de la lumière [Optics essay on the attenuation of light] (in French). Paris, France: Claude Jombert. pp. 16–22.
- ↑ https://archive.org/details/TO0E039861_TO0324_PNI-2733_000000 Lambert, J.H. (1760). Photometria sive de mensura et gradibus luminis, colorum et umbrae [Photometry, or, On the measure and gradations of light intensity, colors, and shade] (in Latin). Augsburg, (Germany): Eberhardt Klett.
- ↑ https://books.google.com/books?id=PNmXAAAAIAAJ&pg=PA78 Beer (1852). "Bestimmung der Absorption des rothen Lichts in farbigen Flüssigkeiten" [Determination of the absorption of red light in colored liquids]. Annalen der Physik und Chemie (in German). 162 (5): 78–88. Bibcode:1852AnP...162...78B. doi:10.1002/andp.18521620505.
- ↑ http://dx.doi.org/10.1016/j.jqsrt.2017.06.038 I.E. Gordon, L.S. Rothman, C. Hill et al., "The HITRAN2016 Molecular Spectroscopic Database", Journal of Quantitative Spectroscopy and Radiative Transfer 203, 3-69 (2017).
- ↑ Calculated using atomic and molecular polarizabilities taken from David R. Lide, "CRC Handbook of Chemistry and Physics: 71st Edition 1990-1991", CRC Press (1990)