Conventional Guns

	Notice:
	Please bear with us. Your ride's still a work in progress.

Introduction

Conventional Guns denotes weapons which propels a mass (shot, projectile) using the exothermic decomposition of a chemical propellant (or charge) in a controlled manner, with propellant being constrained inside a barrel (as opposed to co-moving with the shot, as is the case with rockets). Having evolved from porcelain filled bamboo tubes that expel shrapnel using the explosion of gunpowder, attested to in the 12th Century in China, and subsequently introduced to Europe by the 14th Century, its prominence in literature that touches on military matters has been remarkable. Therefore it is not surprising that conventional guns continues to feature in many science fiction with a focus on warfare, although these depiction has seldomly been fair. Quite often, conventional gun technology has been treated as one of lower technological sophistication, that cannot hope to compete with other weapon systems (such as railguns, coilguns, and especially with missiles), and authors have often resorted to "too clever by half" twists that supposedly circumvent limitation of conventional gun, only to miss important caveats and leave out more plausible advances that may come either as natural consequences of the prevailing technological advancement of a setting, or as potential advances with some effort.

In any case, whatever the reason for this deplorable state of affairs may be, in line with Galactic Library's goal of providing literature where other sources fail, this article will seek to explore the design space of conventional guns with the help of interior ballistic theory, with a special focus on its impact for science-fiction worlds, and outline some real-world advanced techniques that promises to further improve upon this basis. Naturally, this will have particular impact on settings that are more near-future.

Theory of Interior Ballistics

Perhaps one reason for the general lack of interest, even in sci-fi interest groups, that conventional guns garner, can be attributed to the sheer complexity of the associated theory that describes the acceleration of shot under combustion of a propellant, known as the theory of interior ballistics. The nature of the process precludes simple and elegant equation like the analogous "Rocket Equation" for rocketry that encapsulates the essence of rocket kinematics. Instead, accurate models are always solved numerically. Thus this article will only go over the details of interior ballistics in so much as it lends to an intuitive understanding of the kinematics of gun systems, or as pertinent to establishing performance figures, and refer the reader to more systematic treatment of the same in reference section for the process of arriving at the detailed calculations later on. Notation in this article generally follows the Eastern tradition as established by M.E.Serebryakov, although the following argument has been much improved by consulting the work of J.Corner as well.

The Propellant

Propellants that are suitable for conventional guns must exhibit a stable burning (in this context, burning means exothermic decomposition in the absence of (appreciable) atmospheric oxygen) behavior. This is best illustrated by briefly going over the history of Nitrocellulose, the primary ingredient in almost all propellant up until rather recently.

When first synthesized circa 1845, Nitrocellulose was found to detonate violently, where upon ignition, a mechanical shockwave is rapidly setup, that propagates in all directions, compressing the material in front to the point of ignition as well. The shock front propagates at a few km/s, limited only by the (compressed) speed of sound in the combustion products, rapidly consuming all propellant. Thus, for 40 years, it was employed as an explosive, despite its advantage over black powder (thrice as much energy density, very little solid product and decreased sensitivity) being clearly evident. It was not until the mid 1880s that Nitrocellulose was tamed by dissolving it in a suitable organic solvent, such as alcohol or ether, that causes microscopic swelling of the micro structure of the fiber. In this state, the propellant behaves like a putty that can be extruded or cast to the desired shape. This leaves microscopic holes, or pores after the solvent is driven off through heat. Now, the behavior of burning changes completely: When ignited, the propellant is heated, at the surface, by the radiated heat of the exothermic combustion products. This causes burning to (largely) happen along a parallel plane to that of the initial shape, with the rate limited by the bulk thermal conductivity of the propellant, to around a few cm/s, at gun pressures, a reduction of five orders of magnitude. This development allowed Nitrocellulose to rapidly replace black-powder as the preeminent component in gun propellants in the next decade, relegating the latter to be used as an igniter and ignition booster for the most part.

A brief discussion of further development of propellant science since that period to that of modern time is given for the sake of completeness, to spare the reader of tracking down fragmentary information across multiple, cryptic DTIC reports and digging through Internet Archive.

In the decades immediately following, Nitroglycerin was added to the mix and the propellant is dissolved in the common solvent Acetone, greatly increasing both the energy density and flame temperature (and errossiveness) of propellant. This being known as the double-base propellant, the original formulation became retroactively known as single-base propellant. In the wake of WW1, the German innovation of using a Nitroglycerin - Ethyl Centralite mixture as both a component of the final propellant and a solvent to cause swelling, eliminating the time and expense necessary to extract the solvent. This "solvent-less" gun powder was rapidly adopted, and especially useful in rocket motors where it would have been extremely difficult to extract solvent due to the thickness of the cast involved. Immediately prior to WW2, another German innovation, that of a modified double base propellant where Nitroglycerin was replaced in part or in full with Diethylene Glycol Dinitrate (DEGDN), both relieved the war-industry of the burden of Nitroglycerin production (which depended upon foodstuff) while also improving the thermal-chemistry of propellant gasses, with overall lower molecular weight, facilitating either increased force or reduced temperature. The downside is reduced thermal stability, much noticeable in hotter climates. At around the same time, the use of Nitroguanidine as the primary energetic component, forming Triple base propellant, increased performance further.

As of late, modified double-base propellant and triple-base propellant appears to be the choice when performance is required of gun system, and expense can be spared in pursuit of the same, while single-base propellant remains dominant for small-arms purposes, or when a certain measure of economy needs to be exercised. Reflecting their usage, the former two usually comes in grains of defined shape and perforation, sized to suit their gun, while the latter tends to be extruded or grinded down into simpler geometry like strand or ball, in standardized dimensions.

Although attempt has been made since then to replace triple base propellant with Mixed Nitrate Ester propellant of greater availability, and indeed various mixture had been type classified, composed of Nitrocellulose mixed with varying proportions of BTTN, TMETN, TEGDN and DEGDN, this appears to not have been widely adopted, perhaps due to a lack of necessity. Finally, it bears mentioning the composite propellant, consisting of a heterogeneous mixture of oxidizer and fuel particles. This appears to not have been adopted for internal ballistic use as much as it is prevalent in rocketry (various Aluminum Percolate Composite Propellant, or APCP comes to mind), due to its lower performance than pure CHON systems.

In recent years, two of the more promising lines of research that bears special mention includes the work on Nitramine propellant, and that of highly energetic poly-Nitrogen Compounds (otherwise colloquially known as Nitromemes in relevant interest circles). The premise behind Nitramine propellant is simple enough: that of taming RDX (Hexogen, Cyclonite) and HMX (Octogen), well known and highly energetic chemical explosives, for use as propellants. It was found that by grinding RDX particles down to 5 micrometers or so, and suspending these particles in plasticizes, these energetic materials could be made to combust stably enough for use as propellant (specifically, this brings the burn rate pressure exponent below 1). RDX based propellant development effort has already bore fruit, with formulations being type classified by the 1980s to 1990s, while HMX based propellant is still under investigated. Work on denser, and even more chemically favorable polycyclic nitramines like CL-20 (also known as HNIW) based propellant is well underway as well.

Another, more speculative line of research concerns poly-Nitrogen compounds. While Nitrogen allotropes, whose names grows in exoticism with the number of atoms being forced together, from Trinitrogen (N3) and Tetranitrogen (N4), to the likes of Hexazine (N6), Octaazacubane (N8), and Bipentazole (N10), are generally considered too unstable for use as propellant (indeed many aforementioned species are considered meta-stable with lifetime measured in seconds). If these can be made to be somehow stable in storage, and dissociate at a reasonable rate after ignition, the much higher density of energy stored within coupled with reasonable molecular weight (the primary product will be N2 (gas) at ~28, as compared to 23-25 of current propellant) would expectantly produce gun system of tremendous performance. However, there is no research at present hinting at how this might be achieved. As a concession to practicality, less energetic compounds can be had with the addition of C,O,H,F to high enthalpy Nitrogen, creating chemically stable structures. It is possible that with the use of inert binders and by applying similar techniques to that of stabilizing Nitramine propellant discussed above, these could be made to burn at reasonable rate, although this too remains in the realms of speculation.

Six propellant properties are relevant to interior ballistics. A brief technical discussion of these is given here. A few assumptions bears mentioning. First, it is usually implied in ballistic work, that the propellant being treated is chiefly a system of equilibrium involving Carbon, Oxygen, Hydrogen and Nitrogen. In this system, the most important reaction at relevant conditions is the water-gas balance (CO + H2O <-> CO2 + H2), therefore peculiar properties of this reaction forms the basis of certain shortcuts we take to simplify our analysis. Second, we have assumed that the properties of gas is constant throughout its entire time in bore. This is analogous to the concept of "Frozen Flow" in rocketry, where detailed theramlchemical calculation is done for "representative condition" (or at best a few conditions, taking an appropriate average), and the gas is taken to not deviate too much from equilibrium. This approximation is justified by working out the reaction rate of the chemicals involved, which is so fast for conditions near the peak pressure point that equilibrium is almost guaranteed, and quickly drops off as the gas cools to below 2000K, at which point reaction almost completely ceases. This also prevents the formation of re-combination products like Methane (CH4) that would otherwise have greatly impacted the result. Of course this is merely a general trend, and calculations can always be improved by incorporating these effects, with diminishing return on effort invested.

• Propellant Force $f$, also known as specific impetus, measured in unit of energy per unit of mass. This is the analogous property, in ballistics theory, to the concept of specific impulse in rocketry. Unfortunately, it has a more tortuous definition of either "the difference between the enthalpy and energy of gas product at adiabatic isochoric flame temperature $T_{v}$ for one unit mass of propellant burned", or equivalently, "the work done by an unit mass of propellant ideal gas expanding in an adiabatic and reversible way from the adiabatic isochoric flame temperature $T_{v}$ down to 0K". By definition, propellant force is:

  $f={\frac {R_{0}T_{v}}{M}}$

  Where $R_{0}$ being the gas constant in appropriate unit, $\gamma$ for the adiabatic index (ratio of specific heat) and $M$ the average molecular mass of gas product. It must be noted here that since the exact stoichiometry does vary, propellant force is strictly speaking, weakly dependent on the loading condition of the gun. Fortunately, as the water-gas reaction is balanced on both sides in terms of gas molecules, this primarily impacts the dissociation reactions. The variation, then, is on the order of few percents for the entire range of conditions seen in practical weapon systems, and only grows large as loading density (see below) drops too low.
  In practice this value is usually derived from peak pressure readings from closed-bomb test according to ballistic theory, with an eye towards representing the condition encountered in its application, which differs slightly from that predicted by thermal-chemical balance calculations. By assuming ideal gas relationship (i.e.$T_{v}=T_{p}\gamma$), this allows relating the (ballistic) propellant force to the (rocketry) specific impulse via:

  $I_{sp}\cdot g_{0}={\sqrt {{\frac {2f}{\gamma -1}}[1-({\frac {P_{e}}{P_{c}}})^{\frac {\gamma -1}{\gamma }}]}}$

  Where $P_{e}$ and $P_{c}$ being the exit and chamber pressure condition, respectively. In the limit of infinite expansion ratio (volume behind shot over chamber free volume) to a vacuum, this approaches:

  $\lim _{P_{e}\to 0}I_{sp,+\infty }\cdot g_{0}={\sqrt {\frac {2f}{\gamma -1}}}$

  This allows a convenient comparison of gun and rocket propellants using the infinite expanded specific impulse. In practice, modern propellants generally have force ranging from 9,500 J/g to 11,500 J/g.
• Bulk Density $\rho _{p}$, or the density of propellant formulation. For most propellant in use this value is around 1.6 g/cc, although propellant with higher density (CL-20 @ 2.0g/cc) is not unknown.
• Covolume $\alpha$, measured in the inverse of density unit, is found in the Nobel-Abel equation of state commonly assumed for interior ballistics work:

  $P(V-\alpha \omega )={\frac {\omega }{M}}R_{0}T$

  Where $P$, $V$, $\omega$ and $T$ are the gas pressure, volume, mass and temperature respectively. This describes the initial observation that gas compressibility rapidly decrease when the volume per mole is decreased close to $\alpha$, with the understanding that $\alpha$ denotes some "intrinsic volume" of the gas molecule that cannot be reduced further through compression. This assumption, while crude, does lend itself to a physically intuitive way of correcting for covolume effects: the relevant "intrinsic volume" is simply deducted from the total to arrive at a "working volume", which can then be substituted into equations derived assuming ideal gas relations. Today, it is known that the reduction in compressibility is actually a much more gradual effect as the mean distance between molecules are decreased, intermolecular repulsion supplant gas kinematics as the primary force resisting compression, with more sophisticated equation of states developed to model such (see below). This correction is practically speaking only necessary for ballistic work, as the effect at rocket pressure (some few tens of MPa) is usually negligible.
  In practice this is usually fitted to a closed-vessel test fire data, making it really an average over the range of condition experienced by gas in chamber. Since, in fact covolume is dependent on chamber loading condition and pressure developed, it is fortunate, then, that its effect is most prominent during the starting phase of ballistic cycle where gun pressure are the highest, and in that range of conditions covolume typically only changes by less than one percent. And although the variation is greater at conditions below that, the contribution is much less, as the effect of covolume is less pronounced at lower pressure in any case. As a result, the experimentally determined value is in agreement to within a few percent of that calculated from the more sophisticated (but developed much later) Virial equation of state, taking the first 3 Virial coefficients and using the highest density encountered.
  For almost all propellant currently used the covolume lies very narrowly in the range of 0.9-1.1 cc/g.
• Adiabatic Index $\gamma$, although the form $\theta =\gamma -1$ is most often used in interior ballistics work. Also known as the ratio of specific heat, or the ratio between the isobaric specific heat and that of the isochoric (constant volume). It is a function of the composition of gas (simpler molecules have higher adiabatic index) and of the temperature (gas at lower temperature have higher adiabatic index) with value ranging from 1 to 5/3.
  Since the equations of interior ballistics can be entirely formulated without the use of constant pressure specific heat, the adiabatic index is often redefined to match the form it appears in relevant work:

  $\gamma ={\frac {R_{0}}{MC_{v}}}+1$

  Which matches the conventional definition only when the gas is ideal. While it is possible to rigorously calculate this value from an appropriate EoS for a certain temperature, in practice the adopted value must adequately represent an average during the expansion of gas, where the gas species can evolve according to (in fact slightly lagging) chemical equilibrium due to the varying pressure and temperature conditions. Consequently, the value used in interior ballistic work is in fact a "slope gamma". J.Corner (1950) suggest taking it between the 1x and 0.7x the flame temperature (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_v} ), while F.R.Hunt (1951) suggests a more elaborate routine involving taking the average of values calculated at a loading density (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta} ) of 0.2g/cc and 1x Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_v} , and a condition of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta=} 0.1g/cc and 0.7x Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_v}
  In addition, it is in some practices customary to increase this value by a few percent to account for the heat loss to barrel, a practice borrowed from that of internal combustion engine modelling (after Cranz). Combustion product at gun conditions (tens to hundreds of megapascals, 2000K-3000K) are well described by a value of ~1.25, even though an exact calculation of the adiabatic index at said condition yields values on the order of ~1.3.
• Burn Rate Coefficient Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_1} and Burn Rate Exponent Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} . The dependency of burn rate upon reaction zone temperature and pressure is a complex topic.
  By examining partially burnt propellant through specially vented chambers, it was established in the 19th century that propellant burning proceeds parallel to the surface of a propellant grain, or in other words, at any time the surface of burnt propellant roughly parallels the surface it had before burning. This observation is known as the Piobert's Law (see above for an explanation), gives rise to the definition of "propellant (linear) burn rate" as the rate at which this parallel surface recedes.
  It is now known that propellant burn rate exhibit several distinct "zones" with each range exhibiting different temperature or pressure dependency, especially in the low pressure ranges (~few tens of MPa). This has been attributed to the transition from solid-phase to gas-phase driven combustion behavior as the latter gets compressed closer to the former. Historically, due to the limitation of instrumentation these idiosyncrasies were not known to a reasonable degree of accuracy, ballisticians have resorted to fitting burn rate to pressure in the range where accurate representation is most important, i.e. at high pressure and close to the operating pressure of guns. By far the widest used representation, is:

  Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u = u_1 P^{b}}

  This is sometimes known as the de Saint Roberts formulation, where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u} denotes the linear burn rate under pressure Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P} . Depending on the exact range of fitted data, the exponent can vary from 0.7-0.9 for modern propellants, and while there are no hard rule to this, it is generally desired to have a exponent of less than unity to prevent excessive pressure spiking, and ~0.7 for rocketry work.
  These two properties are perhaps the least explained of all as propellant performance is concerned. While empirical rules have been developed to describe the burn rate of arbitrary mixtures of some well known propellants , and it is possible, through very detailed calculation, to predict the burn rate of a propellant, this is in practice seldomly done unless very specific features of combustion are being studied. Uncertainties in these areas are also the primary concerns for prospective and hypothetical propellants, since these generally require enough quantities to be synthesized for testing in a closed vessel, and even then sometimes data are only available for very low pressures due to the scarcity of high-pressure closed vessel apparatus capable of performing such experiments.

A brief note on the techniques for estimating these parameters. Recall the water-gas balance (CO + H2O <-> CO2 + H2). It was noted by Hirschfelder and Sherman in the 1930s that, not only is this reaction not excessively influenced by pressure due to having a balance of gas molecules on either side, as mentioned above, but also by a peculiar coincidence of numbers of the mean molecular weight and heat capacity, the propellant force is also relatively insensitive to the ratio of CO2 and H2O. This, then, allows estimation to be made with only the ratio of atoms present within a CHON system, without regard to solving the exact equilibrium and assuming a priori a ratio, of almost all the thermal chemical properties relevant to ballistics. Other properties like covolume can then be fitted to these estimated properties. This is the premise of the Hirschfelder-Sherman estimation technique, whose result are usually within 2-5% of the far more laborious solution.

Otherwise, it is necessary to use the more conventional method that rocket scientists have been perfecting for the better part of a century, with special care of using constant-volume thermal properties instead of the constant pressure ones usually given in relevant databases. By iteratively calculating the chemical equilibrium giving an assumed reaction temperature, calculating the difference between the heat of formation of the product and their predecessor, adding in the internal energy of the reaction product, and revising the temperature estimate based upon this, it is possible to, finally, rigorously estimate these up to the accuracy of the underlying database. This method is detailed in almost every standard interior ballistics textbook and is also used to generate the tables present in this article. (WIP)

The Simplest Gun

The simplest gun system in terms of ballistics theory is one where all the propellant has burned to depletion before the shot has appreciably moved. The shot is then propelled by adiabatic expansion of high pressure combustion product down the bore. An additional simplification introduced here is that the weapon does not have any chamberage (i.e. the chamber is of the same diameter as the barrel, see later for an discussion about chamberage effects). This is hardly a realistic proposition for a practical weapon, as this type of gun would demand excessively heavy and thick chamber to contain the pressure developed in what amounts to the isochoric combustion of the propellant gas. Instead, the value of this idealized representation lies in its simplicity. By ignoring the minutiae of burning, it eliminates most theoretical difficulties and reduces the problem of interior ballistic to its central problem: namely, under the constraints of:

• The gas velocity, for a small group near the breech face, must average 0.
• The gas velocity, for a small group near the bottom of the shot, must average the shot velocity.

determine the distribution of group velocity, pressure and density along the barrel. This problem, named for the great polymath that first formulated and attacked it, is often known as the Lagrange problem in interior ballistics. Various attempts has since been made by postulating some initial distribution of

The Lagrange Approximation

Lagrange, having formulated this problem in 1793, attempted to simplify it by introducing an additional assumption, that the gas density is constant throughout the entire volume. The implication of this is explored more fully by Piobert and later Sebert (late 19th C.). Substituting into the equation of continuity:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d\rho}{dt}+\frac{\partial \rho}{\partial x} v_g + \frac{\partial v_g}{\partial x} \rho = 0}

Using Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_g} to denote the velocity of gas. Noting that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial v_g}{\partial x} = 0}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\rho} \frac{d\rho}{dt} = - \frac{\partial v_g}{\partial x}}

Integrating on both sides yields:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_g = \frac{x}{l}\frac{dl}{dt} }

Implying the gas velocity is linearly distributed along the length of barrel between the breech face and the shot base. It then follows that the pressure is distributed in a quadratic manner along the gas volume:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_x = P_s + \frac{\omega}{2m}[1-(\frac{x}{l})^2]\cdot(P_s-P_r)}

Where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_x,P_s,P_r} denotes gas pressure at location Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} along the barrel, the pressure at shot base (s stands for shot), and the resistive pressure acted upon the shot, respectively.Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l} is the shot travel at that point. It is also customary to express drag simply as a ratio of shot base pressure: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1 - \frac{P_r}{P_s})^{-1} = \varphi_1} . In particular, the breech pressure Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_b} when taken at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=0} is:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_b = (1 + \frac{\omega}{2 \varphi_1 m}) P_s}

Evaluating the integral Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{l}\int_{x=0}^{x=l} P_x } , the space-averaged pressure is:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P = (1 + \frac{\omega}{3 \varphi_1 m}) P_s}

The ratios Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda_1 = \frac{1}{2}} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda_2 \frac{1}{3}} that appears in the above equations are known as Piobert's constants, values whose physical meaning will be explored in the later paragraphs.

The length we have came to discussing the specifics of the Lagrange approximation is due to the remarkable agreement with reality. It is now generally accepted that the assumption of uniform density is enforced by the presence of pressure waves that reflects between breech face and shot base, tending towards equalizing the density along its way, towards the uniform value that the Lagrange assumption presuppose. Of course, this only explains how a condition of uniform density might be developed, without regard to the actual initial condition of the gas, which motivated others to examine more "physically plausible" configurations that can naturally develop, see below.

From this, we can also glimpse the limitations of Lagrange approximation. As the charge to shot weight ratio increase, it can be shown that these pressure waves (if there were to be such disturbances) would become increasingly rare, spending most of the time the shot is in bore catching up to it, with the gas exhibiting considerable difference of density along the volume. Then, the Lagrange approximation cannot be thought of as appropriate.

The Pidduck - Kent Approximation

While the Lagrangian approximation is useful as far as practical applications are concerned, there is some interest in developing an approximation that is plausible, that is it naturally derives from certain initial configuration. The Pidduck approximation is really the culmination of a long line of work by Riemann, Hugoniot (1889), Gossot and Liouville (1914), and Love and Pidduck (1921-1922). The premise is simple enough: the pressure, density and temperature are all uniform, and gas behaves adiabatically. Then, rarefaction waves that appears as the shot starts moving are laboriously traced as they refract, finally leading to a pressure distribution at any time behind the shot, the exact solution of which strained the computational capabilities of the time to such an extent that only certain special solutions were attempted. A feature of note is that no shockwaves were predicted in these solutions.

It was noticed by Pidduck (1936) that these initial pressure waves are damped out rather quickly, leading to convergent solutions for when the shot has traveled appreciably. Pidduck's limiting solution refers to one such solution. Kent (1936,1937,1938) derived essentially the same limiting solution via a different method, leading to the solution being associated with both in Western academic sources, although the name of Pidduck is more recognized in Eastern literature.

Since even Pidduck's limiting solution is still rather involved, the details are elided here and the reader is referred to standard textbook in interior ballistics for details. The limiting solution is strikingly similar to that of the Lagrange, as a velocity distribution approaching linear is predicted, although the pressure and density distributions are much complex.

This idea is further developed by M.A.Mamontov (1959), noticing that among others, Pidduck's limiting solution does not actually depend on inclusion of the covolume factor. He instead attacked the problem under the assumption of a uniform temperature field, as it was felt that at higher ratio of charge to shot, it is least unlikely that temperature remain relatively constant, as compared to any other parameters being studied. His solution is now understood as the limit of Pidduck's limiting solution with as adiabatic index approaches unity. Being developed in the Soviet Union, his work is relatively unknown in the West as it was felt that this line of inquiry has been exhausted on a high note with Pidduck and Kent's work.

The closeness of various approximate solutions to the Lagrange problem can best be appreciated by listing the respective Piobert constants for each.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda_1} From Ballistic Approximations Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\omega}{\varphi_1 m} } 0.2 0.4 0.6 0.8 1.0 1.5 Lagrange 0.500 Pidduck (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma=1.25} ) 0.494 0.488 0.483 0.479 0.475 0.466 Mamontov 0.492 0.485 0.479 0.474 0.469 0.458

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda_2} From Ballistic Approximations Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\omega}{\varphi_1 m} } 0.2 0.4 0.6 0.8 1.0 1.5 Lagrange 0.333 Pidduck (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma=1.25} ) 0.327 0.321 0.316 0.311 0.307 0.298 Mamontov 0.325 0.318 0.311 0.306 0.300 0.289

It must be stressed that the agreement of multiple theories does not imply agreement with reality. In fact, the theoretical justification for all approximations detailed above are strongest when charge to shot weight ratio is small, disagreeing with each-other (and with experiment) as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\omega}{\varphi_1 m} } increase. Experience has demonstrated this agreement as "excellent" below 0.5, and these have been applied in literature, apparently without fanfare, to modern APFSDS rounds whose value approaches unity.

Solution for the Simplest Guns

Many similarity relations exist in the study of interior ballistics. For the simplest gun, having determined the propellant, only few parameters are required for establishing its performance. These are:

• Effective Charge to Shot Mass Ratio, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\omega}{\varphi_1 m}} .
• Loading Density, or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta = \frac{\omega}{V_0}} , the mass of charge divided by the total chamber volume. It bears mentioning at this point that for interior ballistics purposes it is customary to ignore any air trapped in chamber as air density is considerably lower than that of the propellant's density, even accounting for the inefficiencies of packing a geometrical shape within a tube. This is usually taken to be around 50% to 60% of the bulk density of a propellant, or around 0.5-0.7 g/cc for large caliber weapons and approaching 1g/cc for small arms.
• Barrel Expansion Ratio, or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda_g = \frac{V_b}{V_0}} . Since we have chosen to neglected the effect of covolume, this is simply Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda_g = \frac{l_g}{l_0}} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l_0 = \frac{V_0}{S}} . Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_b} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_0} are the barrel volume and chamber volume, respectively, while Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l_g} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l_0} denote the length of gun to the length of chamber, finally with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S} the cross sectional area of the barrel.

It should be fairly evident that if the gun solution can be expressed in these parameters, by examining the variation of performance with these parameters one can generalize the findings by substituting in the specific values for shot mass, loading density and of barrel expansion. For the following analysis, the ballistic solution of a hypothetical propellant of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_{sp} = 300} s, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma = 1.25} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_p = 1.6} g/cc, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha = 1.0} cc/g will be considered. These are rather standard values for propellant used today.

Now, it is finally time to tie in all that we have discussed and examine the problem of the simplest gun. The initial condition (as far as the shot is concerned) has the propellant fully combusted, and since the shot has not appreciably moved, the volume the combustion product occupies is precisely the chamber volume. The gas temperature is then exactly Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_v = M f/R_0} , as defined. Substituting the relevant conditions into the Nobel Abel EoS gives:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_0 = P_m = \frac{f \Delta}{1-\alpha\Delta}}

Since there is no further addition of gas behind the shot, and as the shot starts moving, the pressure can only decrease, it is appropriate to label this point as both the initial value (subscript 0) and the maximum value (subscript m).

As the shot starts moving, not only does the volume increase, but also some energy is extracted from the propellant gas, accelerating the projectile. Recall from our discussion of the Lagrangian problem and especially its approximations, that a constant (for this particular loading condition) ratio between the space mean pressure and shot base pressure exist. It stands to reason that since work is but force integrated over distance, and that both gas and shot starts with no (macroscopic) kinetic energy, this would cause the kinetic energy of the two to be related. Indeed it can be verified through the use of calculus (this assertion is usually left as a homework for students of interior ballistic, since it involves only rote application of conventional integration rules), that the total kinetic energy of the shot and gas can be expressed as:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\varphi m v^2}{2}} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varphi = \varphi_1 + \lambda_2 \frac{\omega}{m}}

Now, noting that the energy must be conserved between the internal energy of the gas, the kinetic energy of the gas, and finally the kinetic energy of the shot. For ideal gas, the specific heat at constant volume, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_v} , is:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_v = \frac{R_0}{\theta M}} , with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta = \gamma-1}

In fact, this is a function of temperature. It is possible to choose, through an appropriate averaging procedure, a "gun gamma" for this purpose, although even this must be corrected with empirical correction factors. Nevertheless, proceeding with this simplification, this allows us to rewrite the equation above to be more general:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(l,v) = \frac{f \omega - \frac{\theta}{2}\varphi m v^2}{S[l + l_0 (1-\alpha\Delta)]}}

Noting the effect of covolume, the gas relation for adiabatic expansion can be rewritten as:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(l) = P_0 (\frac{1+l/l_0-\alpha\Delta}{1-\alpha\Delta})^{-\gamma} }

With these equations it is now possible to solve for the relation of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P} ,Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v} , though in a rather roundabout manner. Rearranging after Corner, this gives:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v^2 = \frac{2f\omega}{\theta \varphi m} (1-(1 + \frac{l/l_0}{1-\alpha\Delta})^{-\theta})}

This can either be interpreted as predicting the velocity of shot for a gun (with unspecified length) at a certain point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l} , or the muzzle velocity of a gun that is of length Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l_g} , then the factor Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l/l_0} in the above is simply Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda_g} , finally reducing the solution for the simplest gun to the three parameters under study, and properties of the gun propellant chosen.

It should be noted at this point that the factor Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 + \frac{l/l_0}{1-\alpha\Delta}} is simply the expansion ratio (volume behind shot to chamber volume) after accounting for covolume effect, so that loading density and barrel expansion ratio need not be discussed separately. With that fixed, the velocity developed simply increase with the square root of charge to mass ratio, all else being equal. Alternatively, if the expansion ratio is allowed to go to infinity, the velocity developed at a certain charge-to-mass ratio increase, with rapidly diminishing return, up to a certain limit. This limit is found by:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{\Lambda\to\infty} v = \frac{2f\omega}{\theta\varphi m} }

Then, the entire solution space, can be represented in a graphical form as:

Muzzle velocity developed by the simplest gun using the hypothetical 300s propellant, with a loading density of 0.5g/cc at various barrel expansion ratio.

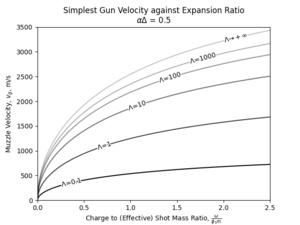
Limits of Performance

Recall that the simplest gun represents the limiting case of a conventional gun where the propellant burns infinitely fast. By generating the highest possible pressure, and allowing for the highest possible expansion ratio for the projectile, the simplest gun also achieves the highest possible muzzle velocity if only the propellant burn rate is varied and all else being equal (the reader is asked to take this for granted for now, a more detailed proof will be provided later). Then, having discussed the performance of the simplest gun in detail, this equips us with a theoretical basis for the discussion of the limit of velocity that can be achieved by conventional gun, in general.

Historically, repeated attempts have been made to derive the limiting velocity that can be produced by the conventional gun, and limits derived using different lines of attack generally disagree. Multiple assumptions sometimes leads to the same limit. With today's hindsight, the three most common "limits" of ballistic performance are, in ascending order:

• the "first ballistic limit", attributed to the experiments of Dr. Heinrich Langweiler (1938), is probably by far the most often quoted. Langweiler considered the gun as a rocket nozzle with unitary area ratio. Then, as the shot weight goes to zero, the shot is simply as fast as the fully expanded propellant gas, which by rocket theory achieves a velocity of:

  Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_{1} = \sqrt{\frac{2f}{\theta}}}

  Which is simply the velocity resulted in by equating the kinetic energy of the propellant gas with heat produced by the chemical reaction. This is also by definition, the infinite expansion ratio exhaust velocity in classical rocket theory, as mentioned above. For our 300s Isp hypothetical example above, this is about ~2900m/s.
  Langweiler was able to then perform a series of experiments, firing increasingly light projectiles out of a small arm using the same weight of fast burning propellant, recording the shot velocity developed in each case. The range of value experimented with was Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega/m = 0.8-44} . Extrapolating to a shot of zero weight, this agreed with his limit to within 1%.
  Despite this agreement, Langweiler's argument is not very strong from a theoretical standpoint. It is not apparent why all the propellant product gas must achieve the fully expanded velocity as implied. Interior ballistic theory, as well as more recent observations, all suggest a distribution of velocity in one form or another, with increased heterogeneity at high Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega/m} . Since this means that Langweiler's limit should be an underestimation, it has also been suggested that this agreement might be coincidental and due to drag in front of the shot, in bore, which is increasingly important at higher velocity and smaller shot weight, effects that Langweiler specifically did not account for.
• the "second ballistic limit" is a simple result of applying conventional ballistic theory, as detailed above, under the Lagrange approximation. Recall the velocity limit of simplest guns when expansion ratio is taken to be infinite. By taking the limit of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega/m \to \infty} , substituting in the relevant Piobert's factors, and expanding Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varphi = \varphi_1 + \frac{\omega}{3m} } , this gives:

  Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_{2} = \lim_{\frac{\omega}{m} \to \infty}\sqrt{\frac{2fw}{\theta \varphi m}} = \sqrt{\frac{6f}{\theta}}}

  Which is ~1.73x greater than that predicted via the first ballistic limit. For our 300 Isp example, this is about ~5100m/s. This improvement is chiefly from the fact that the second ballistic limit took into account that not all gas need to travel at the same velocity. Instead, the Lagrange approximation is taken to hold up to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega/m\to\infty} . This is not necessarily true, though, as experiments (and more sophisticated theories) tends to show a decreasing Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda_1} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda_2} as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega/m} increase, resulting in increased fraction of energy devoted to accelerating the projectile, as opposed to the propellant gas (this also implies that the linear distribution of velocity is also not strictly true at high Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega/m} ). This tends to make the second ballistic limit an underestimation of the true potential of conventional weapons.
• the "third ballistic limit" is similar to the second, although this time applying the ballistic theory under the approximation of Pidduck's limiting solution. Since the mathematical details are unnecessarily complex for the current discussion, only the result will be shown here:

  Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_{3} = \frac{2}{\theta}\sqrt{f(\theta+1)}}

  Which, using the same example, is a further ~1.83x that of the second ballistic limit, or approximately ~9300m/s. Recall that Pidduck's limiting solution represents the limiting behavior of a physically possible evolution of the propellant gas when started from a uniform initial distribution, when the initial pressure oscillations is negligible, conditions which should be reasonably satisfied in the case of an infinitely long barrel as is assumed here.
  The third ballistic limit is also associated with Schardin and Pfriem, whom derived this limit in a rather different way: instead of considering the problem as one of ballistic, they considered it as a hydrodynamic problem, where upon the complete and instantaneous combustion of the propellant, a shot of negligible mass does not impede the creation of a shockwave at the interface between the propellant gas in chamber and the air in bore. It is also assumed that the reflection of this wave does not interfere with the shockfront in the time interval of interest. Then, the maximum possible velocity is simply the particle velocity behind the compression shock. Taking the limit as atmospheric pressure approaches 0, they also arrived at the aforementioned limit.

It is hoped that through this discussion of various types of limits, each based on certain theoretical consideration, it will begin to be appreciated the considerable difficulty of putting a concrete number on the performance limit of conventional guns. Here then lies the dangers of trying to reduce the nuanced view to broad, and generalizing statements.

For example, it is commonly misunderstood in science fiction that some fundamental limit exist that limit conventional weapons to say 2.0-2.5km/s. This may have came about through theoretical argument analogous to that outlined for the first ballistic limit, or alternatively, by extrapolating from similarity based, semi-empirical methods of conventional gun design. Of these methods, perhaps the Le Duc method is the most well known through its dint of having been used in some capacity by the US Navy up until 1942. In Germany, a similar method named after Heydenreich was in use at Rheinmetall up until 1945. It is also possible that this may have came about as an independent, empirical observation drawn from observing recent trend in guns and artillery development. In any case, the origin of this prevailing belief is perhaps lost to us.

What can be known, though, is that if there does exist some performance red line that even fictional improvement in technological prowess are still bound by, it is somewhere between the first, second, and the third ballistic limit.

Optimal Design Problem for the Simplest Gun

Having explored the performance envelope of conventional gun, it is important to note that real weapons are without fail volume constrained. Therefore, a more useful way of considering the performance is to start with a fixed total "tube length", and explore the influence of loading density and barrel expansion ratio on the velocity developed at muzzle, with both the chamber and the barrel volume dependent on the aforementioned design parameters.

Velocity developed by simplest gun with 300s propellant, plotted against charge to mass ratio, under conditions of various total tube length (barrel is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda_u} times the chamber long when loaded to a charge-to-mass ratio of 1 or unity) and loading density.

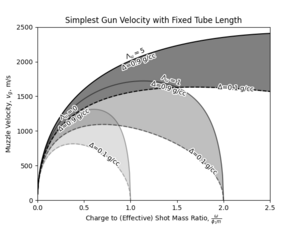
The appearance of optimal charge to mass ratio that maximized velocity developed for a given combination of total tube length and loading density conditions can be explained by the balancing effect of increased charge also reducing the effective expansion ratio by reducing the free volume in barrel. Loading density can be thought of as setting the ratio of these two effects, therefore at higher loading density, the balance is shifted to prefer a greater charge to mass ratios.

Gun with Finite Rate of Burning

Having thoroughly discussed, and developed a theoretical description of the simplest gun, it is now possible to extend this description by relaxing some idealized assumptions. We shall begin with doing away the assumption that the combustion is infinitely fast. Real world propellants have a finite burn rate (see above section on propellant) dependent on pressure, and the area exposed to combustion at any time is a function of the propellant's grain shape. Therefore, the theory that describes the coupling between propellant combustion, pressure developed and shot movement are by necessity, complex.

It bears mentioning that we take the various ballistic approximation as applicable in this section, although notably propellant combustion of a finite rate violates the Pidduck-Kent (and by extension, Mamontov's) argument. A valid argument can be made that in practical guns, the oscillation of the wave system is not damped out in a negligible time frame. In fact, as stated by Hunt (1951), the rarefaction wave predicted by these above works were never observed in practice. Then, the applicability of these assumptions, and consequently the prediction based on these, is always an approximation, and should be taken with an acute awareness of these limitations. In effect, this reduces the faith that can be placed on these sophisticated approximation to no more than what can be given to the simpler Lagrangian approximation, i.e. they are only as valid as they are a close approximation of reality, and this approximation is held to be good for the solution space where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\omega}{\varphi_1 m} < 1 } .

Theory that models the finite rate burning of propellant requires some way of relating the bulk burn rate (as explained in the propellant section) to the evolution of variables such as free volume (or volume not occupied by the charge), and energy added to the gun system. The former, in the interest of preserving the scalability of theory, is best described by taking the derivative with regard to time, for the product of linear burnt extent Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z} and a characteristic length for the grain Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e} , also referred to as the propellant web. For the latter, by convention the the fraction of propellant unburnt using Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi} . The two may then be related through what is known as the form function, so called since its purely a function of the grain geometry. This, together with a choice of bulk burn rate law for the propellant, is collectively referred to as a equation of burning.

When the equation of burning is added to the interior ballistic system of equation, which now consists of the equation of motion of the projectile, and finally the balance of energy equation, the resulting system is not necessarily analytical (i.e. admits a closed form solution), and certainly not simple. Then, the choice of burn rate law and that of form equation must consider both the accuracy of representation, with regard to the practicality of solving these systems.

All told, a great deal of freedom exists in the exact formulation of the equations for interior ballistics, with certain line of attack preferred over others depending on the time, location and resource available, and the nature of insight desired. It is then not surprising that particular solutions are often associated with its progenitor or practitioner by name.

Burning Described by Quadratic Form Function

The quadratic, or the Charbonnier form of the equation of burning was the preferred formulation up to the mid last century, and remains especially popular in the Western world. Its primary strength lies in its success in capturing the theoretical behaviour of relevant geometries to high-powered interior ballistic work, while keeping the complexity of the resulting solution low, through the tuning of one variable, the form factor \theta. It takes the form:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e \frac{dZ}{dt} = B(P)} , and

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi = (1-Z)(1+\theta Z)} , i.e., Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi = -\theta Z^2 + (\theta-1)Z + 1}

Where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B(P)} is some burn rate function of pressure. The "form factor", Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} conveniently takes 0 for a "neutral" geometry, where the area of combustion does not depend on the extent of burning, and takes 1 for a propellant in "degressive" geometry, that is the area exposed to burning is reduced during burning.

The definition of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta } is particular suited to describing propellant of the shapes usually denoted "ribbon" and "flake". The following table summarizes the procedure for a few simple shapes.

Propellant Geometry Described by the Form Factor

Shape	Length	Width	Height	Form Factor
Ribbon $\lambda \gg \mu \gg 1$	$\lambda e$	$\mu e$	$e$	$\theta \approx {\frac {1}{\mu }}$
Flake $\lambda =\mu \gg 1$	$\mu e$	$\mu e$	$e$	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta \approx \frac{2}{\mu}}

A special case is when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta = 0 } , the most common example being the tubular propellant geometry, in which case, experience has shown that a internal diameter no less than 3/4th of the annulus for even ignition on both sides is required. Then, the web is simply the difference between the annulus and internal diameter. The mathematical justification for these shall not be detailed too much here, except by noting that these can be derived from expressing Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi } in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z } and neglecting the higher order terms in the coefficients.

Since by definition, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(1) = 0} and psi(0) = 1${\displaystyle }$, that is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta } must take between -1 and 1. Geometries where the regressiveness of burning is higher than allowed in this formulation, that is when the volume is burnt as a higher order function of the linear burnt extent, a particular example being spherical grains, which burns according to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi = 1-Z^3} . These simply cannot be represented in the Charbonnier form. This, although on first sight a serious limitation of this approach, is in practice mitigated by the relative ease of conducting experiments in the few cases where more regressive propellant are used e.g. in small arms and infantry mortars, out of practical concerns for manufacture.