Propulsion Performance
This is a STUB ONLY -- there is a page in draft for this, I put the blank page up to create a place to link to from other pages -- stay tuned (Rocketguy)
Almost the first question anyone asks about propulsion systems is “What’s the best one?”. If that question had an answer, everyone would already know the answer. You have to add a little more detail and ask “best for doing what?” to even start the conversation. This is a subject that can get pretty complicated, but we’ll start with the basics and work up.
Usually, what you care about in a transportation system is “how long does a trip take” and “how much does it cost”. Let’s start with “how long”.
The simplest case is a trip which is out in space, far enough away from planets and stars that the effect of gravity can be ignored. Even inside a Solar system, this comes pretty close for very fast trips because gravity doesn’t have a lot of time to affect the course. When your cruise velocity is more than about 1.5 times the local escape velocity from the Sun, and the start and end point are on the same side of the Sun rather than crossing near the Sun during the trip, the straight-line approximation works fairly well.
We will work everything in metric units (SI), meters, kilograms, and seconds. One of the challenges in explaining propulsion is that it is easy to get tangled up in the units. That requires familiarity with scientific notation, '((NOTE: do we want to typeset scientific notation or use computer notation, 1.2E23 and so on? Typesetting is a pain but more formal, we should probably make that style decision for use throughout))'. Distances in spaceflight are usually measured in kilometers (1000 meters), miles (1609 meters), nautical miles (1852 meters), astronomical units (AU) ( meters), light years (ly) ( meters), or parsecs (pc) ( meters). Though not in common use, a useful metric unit for interstellar distances is the Petameter (Pm), neters; a light year is then 9.5 Pm.
Consider a trip of about 6.6 AU … a little further than the closest distance from Earth to Jupiter, a little closer than Earth to Saturn. That’s meters. We’ll want to go there and come to a stop, rather than just passing.
A few terms: velocity is the rate of change of distance (meters/second), and acceleration is the rate of change of velocity (meters/second^2).
If your propulsion system provides a high acceleration for a short time, you can treat this very simply: you pick up a velocity change (usually written Δv, pronounced ‘delta-vee’), coast at constant velocity, and make a similar quick braking maneuver at the end. In that case, the time is mostly spent in the coast, and that time comes from the simple high-school physics equation:
d = v * t
Which can also be written:
t = d/v
If the coast velocity is 10000 () m/s, then the time is ( m) / ( m/s), or seconds. (1 year is seconds, or very close to seconds), so the trip takes about 3.16 years (/ = 3.16). The graphs below are for 0.01 m/s^2 acceleration on that voyage during both acceleration and braking, which, over that distance, is very nearly an instant jump to cruise velocity. Missions where you can neglect the distance and time spent accelerating and decelerating are called 'instantaneous impulse' trajectories.
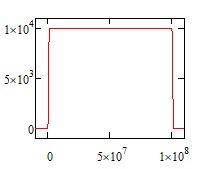 The velocity jumps almost at once to cruise velocity and comes back to zero during braking
The velocity jumps almost at once to cruise velocity and comes back to zero during braking
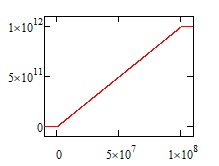 The distance changes at a constant rate defined by the cruise velocity
The distance changes at a constant rate defined by the cruise velocity
Now obviously, the lower the acceleration, the more time it takes to build up to cruise velocity and the more distance covered while still accelerating. If you keep lowering the acceleration, there comes a point where you barely have enough distance to even get to a given cruise velocity; you accelerate to the midpoint of your voyage and then turn around and decelerate the rest of the way. That particular trajectory has a fancy name ("brachistochrone"), and it essentially defines the lowest acceleration you can use and still hit a given peak velocity. If the acceleration is the same during the acceleration and braking maneuver, that is:
minimum_acceleration = (peak velocity)^2 / (voyage distance)
And in this case, the trip takes just twice as long as it would for the same peak velocity but an instantaneous impulse. For the example given, that is an acceleration of 0.0001 m/s^2 ( m/s^2), and you get velocity and distance curves like this:
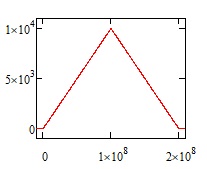 The velocity ramps up to a peak then immediately back down as we start braking
The velocity ramps up to a peak then immediately back down as we start braking
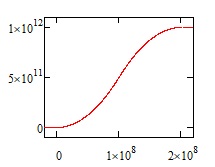 The distance passes more and more quickly to peak velocity and then more slowly as we brake
The distance passes more and more quickly to peak velocity and then more slowly as we brake
((link to a side page on Basics Of Calculus))
Now to make this trip, your propulsion system has to deliver a velocity change (Δv) of 20000 m/s, or twice the Δv just to accelerate. Even that modest velocity is more than a chemical rocket can realistically provide, and yet the trip is pretty slow by most standards. This is one of the reasons why it is very common to use a different system to accelerate than to brake. For example, all Mars missions to date have used rockets to accelerate from the neighborhood of Earth out towards Mars, but have used braking in the Martian atmosphere for at least some portion of the deceleration. That doesn't add much complication; you can just keep track of how much Δv is required for each propulsion system.
Now before getting in to the details of how one estimates performance for each different kind of propulsion system, two general principles are clear -- propulsion systems have limits on how much Δv you can get, and they have limits on how much acceleration you can get, and both parameters matter for working how how long a trip takes and what kind of propulsion system matters.
There is a little bit more we can say about that which applies to all propulsion systems; acceleration capability of a propulsion system and achievable Δv for a propulsion system aren't really independent parameters. One can see this from basic mechanics:
Energy = Force * Distance --- this is the definition of energy
So:
d/dt (Energy) = Power = Force * d/dt (Distance) = Force * (Relevant Velocity)
We haven't said what velocity is involved here, and it's different for different propulsion systems, but clearly, as we talk about more force, or higher velocity changes, more power is involved. And there's a tradeoff between force and velocity -- for a given power, if we want more force (thrust), we have to accept less velocity, and vice versa.
In physics "specific" is a term that means 'per unit mass'. So we can divide both side of this equation by some scaled mass. Let's use the mass of the ship. Then we get:
Power/Mass = "Specific Power" = (Force/mass) * (Relevant Velocity) = acceleration * (Relevant Velocity)
Or, simply, writing Psp for "Specific Power" (in metric, that is watts/kilogram)
Psp = acceleration * (Relevant Velocity)
This is not the most common way of talking about this concept; each type of propulsion system has its own vocabulary. However the parameter usually appears in some form or another -- rocket people talk about "thrust to weight" ratio, and nuclear-electric people talk about "alpha" which is the inverse of specific power (kg/W). The use of Psp as a way to compare dissimiliar propulsion systems emerged in a study on that subject.[1] as a metric that could apply to all of them.
Looking back at the classification box of propulsion methods, many of them involve something that is carried aboard the ship and expended during the propulsion process, whether that be a source of energy, a source of reaction mass, or both (any of the propulsion methods that have an 'internal' source fall in to this category). If that's so, some part of the ship mass is given over to carrying the "thing that gets used up for propulsion" -- generically 'propellant' or 'fuel' or 'reaction mass'. In this case, obviously, there is only so much of the consumable supply onboard and this limits the achievable Δv. It will turn out that the systems that do not carry consumables have their own limitations. In the case of propellant using an internal consumable, it obviously matters how much propulsion we can get out of a given mass of the propellant or fuel or reaction mass.
Δv = acceleration * time
So:
Δv = (force / (ship mass)) * time
The quantity "force times time" is called "Impulse", so we can write this as:
Δv = Impulse / (ship mass)
Now if we are expending propellant, ship mass during the maneuver is not constant. So we can't just ask "how much impulse" did we get; we have to look at slices of time and ask how much impulse we get during each little slice of time. The math to work that out is a bit too complicated to include here (see https://en.wikipedia.org/wiki/Tsiolkovsky_rocket_equation )). But the important thing is that there is a relationship between how much impulse we got, and how much consumable (reaction mass, fuel, propellant) we had to use to get it. Again, we call something 'specific' when it is 'per unit mass', so we can define a performance parameter which applies to all propulsion systems using an onboard consumable:
Impulse / (mass of propellant or other consumable) = Specific Impulse = Isp
From the definition of Impulse, we can write:
Isp = Impulse / (propellant mass) = force * time / (propellant mass)
This has units of velocity -- there's a lot of confusion on this point for historical reasons, but it is clear in the physics. In SI units, Newton-seconds/kg simplifies to meters/second. In various 'English/American Provincial' units, 'if used properly' one would write force in poundals and mass in pounds, and get feet/second, or one would write force in pounds and mass in slugs, and again get feet/second. Sadly, early workers in the rocket field were not so careful about units, and they wrote force in 'pounds force' and mass in 'pounds mass' and cancelled the two different kinds of pound and got specific impulse in 'seconds'. The usage is widespread. We will try at least to clear up the confusion by writing "Isp/g0" when we want to talk about 'seconds' (where g0 is a standard Earth gravity, the difference between a 'pound of force' and a 'pound of mass'). Airbreathing engines define a different unit of "specific fuel consumption" based on lb/hour rather than lb/s of fuel, which is even more confusing, but it can be converted to Isp.
Just what physically corresponds to that 'characteristic velocity' we call Isp is different in different propulsion systems -- but for performance purposes, it doesn't matter. Whether it be fuel in an airbreathing engine, propellant in a rocket, or reaction mass being expelled from some other energy supply onboard, if you're using something up to get your propulsion, Isp defines how much propulsion you get for each unit of consumed mass.
- ↑ Millis, Marc G., Jeff Greason, and Rhonda Stevenson. Breakthrough Propulsion Study: Assessing Interstellar Flight Challenges and Prospects. No. HQ-E-DAA-TN60290. 2018. retrieved from https://ntrs.nasa.gov/api/citations/20180006480/downloads/20180006480.pdf











