Energy Storage
Science fiction is full of flashy technology. Incandescent beams. Hover sleds. Menacing robots. Spaceships with obscure engines pumping rocket plasma into the void of space. Unexplained glowing things cluttering up engineering bays and mad scientist's workshops. But all these things need energy. And if you are not making use of the energy as soon as it is generated, you need to store it. Here, we'll discuss some of the ways that energy can be stored in order to power all of these wacky tech ideas.
Electrical energy storage
Batteries
Batteries store energy in chemical reactions or aqueous ion migrations that drive currents of electrons. Batteries store more energy than other modern electric storage technologies, but release it more slowly. This makes them the go-to solution for current electrical technologies such as electric vehicles, hand-held cordless power tools, and grid-level electricity storage. To get a reasonable rate of fire out of something like a directed energy weapon, you will need large battery packs to meet the average power requirements – but that large battery pack will give you a very large number of shots. A battery for a pulsed power application (such as a pulsed laser, particle beam or electromagnetic gun) will almost certainly be energizing a faster discharging electrical circuit element like a capacitor or an inductor.
Lithium-ion battery
The modern standard is the lithium-ion (Li-ion) battery. These batteries store lithium ions packed between the atomically thin layers of a graphite anode. When the battery discharges, the ions migrate through an electrolyte to be absorbed into a metal oxide cathode layer (usually cobalt oxide, for the high energy storage, but iron phosphate or manganese oxide are also used). When the battery is recharged, the lithium ions are dragged back out of the cathode material and pushed back into the graphite. As of 2021, commercially available Li-ion batteries can store somewhere between a third and one MJ/kg, and discharge at a rate of about a quarter to a third of a kW/kg. They have a self-discharge rate of about 2% per month, a charge-discharge efficiency of 80 to 90%, and last for something like 1000 charge-discharge cycles.
Lithium metal batteries
Lithium metal batteries are a potential near future battery technology. They replace the graphite anode of the Li-ion battery with a layer of lithium metal. In combination with a solid state electrolyte, they might get specific energies of about 2 MJ/kg, or twice as much as a Li-ion battery. We can make lithium metal batteries today, but they can only handle several dozen charge-discharge cycles before shorting out (and potentially catching fire!). There's a lot of research trying to find ways to make them last longer and be safer. By the time we're ready to equip our troops with laser rifles, we might have ironed out these difficulties.
Lithium sulfur batteries
Lithium sulfur batteries replace the cobalt oxide cathode of a Li-ion battery with sulfur. Sulfur weighs less than cobalt, so you can cut down on the weight even more. How much more? We don't know yet. Most of the research these days involve ways of keeping the batteries from getting clogged up with unwanted lithium-sulfur compounds, greatly limiting their life. Maybe some sort of lithium metal sulfur battery with a solid electrolyte could reach 2.5 or even 3 MJ/kg? We'll eventually figure it out, but in the meantime we'll need to be patient and wait for the researchers to do their stuff (or, you know, because we are making science fiction, make something up).
Lithium-air batteries
Lithium-air batteries might be the ultimate in battery technology. You would have lithium metal at the anode and lithium oxide at the cathode, with a current of lithium ions being passed between them through the electrolyte and the current of electrons giving you your electric power is what balances the charges. Up to 6 MJ/kg has been demonstrated in the lab (as of 2021); but the theoretical maximum specific energy is 40 MJ/kg! This, of course, is excluding the weight of the oxygen, which is assumed to be freely available from the air. But for all their promises, there are many challenges. Both their charging cycle lifetime and charge-discharge efficiency are disappointingly low, meaning that they will probably remain in the laboratory rather than store shelves for some time to come.
Storage batteries
Sometimes you are not mass-limited in your application. You don't care about super-high specific energy but just want the most energy storage for your dollar. A common application like this is grid-level energy storage, where your batteries won't be moving anywhere but just sitting in a shed someplace so no one really cares how big they are as long as they are cheap.
Flow batteries are a strong contender for applications like this. They have tanks of two kinds of liquid electrode that can be pumped past an ion exchange membrane. The capacity of the flow battery can be easily scaled up by just adding bigger tanks. They also tend to have high charging cycle lifetimes and if the electrode liquid gets degraded anyway it can be replaced without throwing away the entire battery.
A number of other battery chemistries have been considered for this role. Iron-air batteries (rust batteries) are one possibility. As of 2024, they have been commercialized and installed in several facilities, advertised as capable of storing grid power for 100 hours[1].
Another possibility is nickel hydrogen batteries. These batteries are known for lasting for an exceptionally long number of charge-discharge cycles, are among the most robust batteries out there, and work even in extreme temperatures where other batteries fail. For this reason, they are often chosen for use in satellites and other spacecraft. They are being investigated for use in long term energy storage[2]
Capacitors
Capacitors store energy using the physical separation of electric charge, usually by collecting positive charge on one plate and negative charge on another, which are held close to one another but separated by an insulating gap. The charges are attracted to the other plate, but they cannot cross the gap between them. If connected to a load, the charge can flow across the load to the other plate to equalize the charge imbalance. This flow of charge (an electric current) can do work to do things you need the electricity to do.
In practical capacitors, the "plates" are more like stacks of foil separated by thin insulating layers and rolled up into a cylinder. If the insulator layer can be polarized by the tug of the electric charges, this polarization can significantly increase the stored energy for a given voltage across the plate, giving a dielectric capacitor.
The energy stored in a capacitor depends on its capacitance and the voltage across the plates. The maximum voltage across the plates depends on the thickness of the insulator layer and the insulator's breakdown field; if overcharged the capacitor will arc, burning a hole through the insulator and shorting the plates which ruins the capacitor. This limits the energy that can be stored in any given capacitor. Increasing the gap between the plates increases the voltage you can get before breakdown, but reduces the capacitance such that you end up getting no net change to energy stored for the same amount of stuff in your capacitor.
The energy stored in a capacitor is E = ½ C 𝒱², for C the capacitance and 𝒱 the voltage across the plates. The capacitance is C = ε ε0 A/d for plate area A, distance between the plates d, ε0 = 8.8541878188×10−12 F/m is the vacuum permittivity, and ε the relative dielectric constant of the insulator separating the plates. For a given breakdown electric field F the maximum voltage you can get before breakdown is 𝒱 = F d. Put these together and the maximum energy density the capacitor can hold is E/V = ½ ε ε0 F2 and the maximum specific energy is E/M = (E/V)/ρ for mass density ρ.
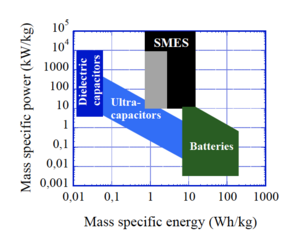
Modern capacitors generally store far too little energy per mass and per volume to be useful for directly storing energy for long term applications, such as powering an electric vehicle or power tool. They do, however, excel at delivering what energy they store very rapidly, allowing very high specific powers. There is generally a tradeoff between energy stored and the power that can be delivered but state of the art at around the year 2010 gives specific energies on the order of 2-3 kJ/kg with specific powers of around 2-3 MW/kg (for discharge times of around 1 ms), or 200-500 J/kg with specific powers of around 200-500 MW/kg (for discharge times of around a μs)[3].
Capacitors can survive many more recharging cycles than batteries, but their charge tends to trickle off on a time scale of a few weeks if left unused.
There is one potential option for capacitors that can store large amounts of energy. Barium titanate (BaTiO3) and certain other closely related perovskite minerals are extra-ordinarily polarizable, giving an extreme dielectric constant on the order of 10,000 or so. It's breakdown field tends to be somewhere in the 150-300 MV/m range and its density is around 6 g/cm3. Directly applying these values without considering the nitty gritty engineering details suggests a possible energy density on the order of a few MJ/liter and a specific energy on the order of several hundred kJ/kg. This is getting close to the values of Li-ion batteries. However, the depolarization time of BaTiO3 is on the order of a second allowing it to discharge in approximately that time. This means that not only do you get a power density of a few MW/liter and a specific power of several hundred kW/kg, but you also can recharge your batteries in only a few seconds if you can deal with the wallplug power to do so. In reality we haven't been able to achieve these optimistic promises, but this is a potential future technology for science fiction that could provide both reasonable energy storage and high power.
Supercapacitors
Also called ultracapacitors, supercapacitors store energy in the separation of charge that occurs at interfaces via various complicated mechanisms like redox reactions, formation of electric double layers, or intercalcation. They are somewhat intermediate between batteries and standard capacitors; able to discharge much faster than batteries but not as fast as normal capacitors, and also can store more energy than a normal capacitor but less than a battery. If you are limited by power rather than energy but still need more energy than normal capacitors can provide you might choose supercapacitors over batteries - you'll be able to shoot your laser blaster more rapidly, but with fewer shots. Supercapacitors can also survive many more recharging cycles than modern batteries, but lose their charge faster (losing most of their charge in a few weeks). The very best modern (2021) commercial supercapacitors store somewhere around 50 kJ/kg and discharge at a rate of about 15 kW/kg. So for high power pulsed applications (like many directed energy weapons) you will still want to accumulate that electrical energy in a solenoid or dielectric capacitor for a higher power but brief discharge that lets you reach the peak power needs of your device. However, laboratories around the world keep hinting at even higher capacity supercapacitors that can store even more energy, so who knows what the future will bring.
Superconductive magnetic energy storage
Main article: Superconductive_Magnetic_Energy_Storage
Inductors, like capacitors, are electrical components that can directly store electrical energy and discharge it quickly[4]. Unlike a capacitor, which stores electrical charge, an inductor stores electrical current which is maintained by electromagnetic induction opposing any changes in the current. In the real world, electrical resistance means the current will decrease over time and eventually fade away to zero – unless you can get rid of the resistance! This is possible with exotic materials known as superconductors, which have no electrical resistance at all. In this way, a superconductive inductor can store a persistent supercurrent that does not fade with time until it is connected to an exterior load and its energy is used. This is called Superconductive Magnetic Energy Storage (or SMES) because the energy can be considered to be stored in the magnetic field produced by the currents flowing in the inductor.
All known superconductors can only remain superconductive at cryogenic temperatures, generally requiring liquid nitrogen or liquid helium to work. Room temperature and pressure superconductors may be possible, but we haven't discovered any yet and it is also possible that none may exist at all. If room temperature superconductors do exist, you could run a SMES unit without any additional cooling.
One of the strengths of SMES is that they can discharge their energy nearly instantly, giving them exceptional specific power. Merely switch the current path from looping endlessly through the inductor to flow through the thing you are trying to power. SMES is limited in its ability to store energy by the usual material limits imposed by the strength of the stuff used to hold the SMES unit together – the currents and fields in the inductor act to try to blow the inductor apart and you need material strength to hold it together.
If you are confining yourself to modern tech, SMES made from REBCO superconductors held together with the best carbon fiber backing material may be able achieve a specific energy of between 2 and 4 MJ/kg. Switching equipment, insulation, refrigerator pumps, helium recovery systems, quench protection, and other equipment will reduce these values somewhat, but if a low mass, compact SMES was desired, performance in the range of 2 MJ/kg and 0.5 MJ/liter may be achievable. This will invariably result in some energy loss as refrigerator pumps are used to keep the superconductors cool, but with large systems this energy loss can be reasonably tolerable for many applications.
In the far future, you might imagine that room temperature superconductors have been discovered. This will likely increase the energy density by at least an order of magnitude. So you might have between 3 and 20 MJ/liter, or even much higher! The ultimate limit of the specific energy will be given by the tensile strength of the backing material, which for atomically perfect graphene or hexagonal boron nitride might get you 45 or so MJ/kg for a rechargeable unit, or maybe even 120 MJ/kg if you only ever intend to use it once. You might want to include a safety factor in this, to prevent it bursting on you if anything jostles or damages it, however!
Mechanical energy storage
Flywheels
Flywheels use the inertia of a spinning disk to drive a mechanical load[5]. To recharge, a motor is used to spin the disk back up. The limit to how much energy it can store is when the centrifugal force at the rim exceeds the strength of the flywheel material and the flywheel tears itself apart. The specific energy of the flywheel is thus limited by the material limits of the disk. But that's just for the spinning disk. For applications requiring electricity, you also need your electric motor/generator. For pure mechanical applications, you will need a clutch and driveshaft and gearbox and transmission. On top of that, you will need a housing (to reduce losses due to air friction by keeping it in vacuum, and to protect the outside world in the event of a failure) and low-friction bearings to allow the flywheel to keep spinning as long as possible. Self-discharge is quite high. With magnetically levitated bearings, self discharge rates are typically about 1% per hour (compared to 10 to 50% per hour for mechanical bearings). Superconductive bearings (which with today's materials must be cryogenically cooled - another source of loss with the addition of a cryogenic liquid logistics train) can reduce this to about 0.1% per hour (or something like 2% per day). But this all assumes that the bearings are only supporting the weight of the flywheel, not any gyroscopic precession torques. Any motion that tends to move the spin axis will lead to gyroscopic effects that will make the flywheel very hard to point and maneuver and also greatly increase the self-discharge rate. Mounting the flywheels in counter-spinning pairs will solve the first of these two problems, but not the second. If you are designing for any kind of mobile application, you will need to put the flywheel energy storage system in gimbals to allow the spin axis to remain constant. Even for stationary applications, you need to be sure the flywheel spin axis is aligned with the planetary spin axis to avoid daily precession cycles. On the plus side, flywheels allow for nearly unlimited charge-discharge cycles without any degradation.
Flywheels are one of the most promising current choices for pulsed power supplies. The flywheel drives an electrical generator called a compensated alternator; the system as a whole is called a compulsator. Compulsators are capable of dumping all of their energy within 1 to 10 milliseconds. Modern (2024) compulsators are capable of storing and rapidly delivering specific energies on the order of 10 kJ/kg and specific powers on the order of 1 to 5 MW/kg[6][7]. The same references [6][7] also suggest future systems could reach 25 to 50 kJ/kg and 5 to 16 MW/kg, so sci fi setting designers should note that there is certainly room for improvement from modern designs.
Springs
Hypothetically, something like a watch spring could be used to drive a mechanical device or run an electric generator[8][9]. To recharge, a motor would wind the spring back up again. Springs are subject to material limits on specific energy, but they are more restrictive than for technologies like SMES or flywheels. The energy density you can store in a distorted solid is one half the stress σ (pressure, tension, shear, etc.) times the strain ε (fractional change in length)
The specific energy is the energy density divided by the mass density ρ
For example, a hypothetical material with a yield strength of σ = 1 GPa and a mass of ρ = 1000 kg/m² could store a specific energy of 1 MJ/kg when used to build a flywheel rim, if it could only elongate by 10% before failure then as a spring it could store at most 5% of that, or 50 kJ/kg. While this example is highly simplified (springs are going to involve tension, compression, and shear, each of which will have different yield strengths) it shows that for good spring storage what you want are high yield strengths, low densities, and high elongations before failure. A high quality spring steel might be able to store about 10 kJ/kg as a spring, Kevlar might store about 45 kJ/kg, while a hypothetical perfect carbon nanotube yarn might be able to support around 2 MJ/kg. Springs also have the usual specific power limits from the electric motor or mechanical drivetrain. You have the benefit of nearly no self-discharge, and no need to worry about gyroscopic forces. However, this is a largely untested technology and its limitations are not well understood yet.
Compressed gas
One way to store energy is to use it to pump a gas into a container to hold that gas at higher pressure. Then, when you need to get the energy back, you can let the gas squirt back out and turn a turbine to generate energy again.
When you compress a gas, its temperature increases. Some of the work you do will go into increasing the gas's pressure, while some will go into increasing its temperature. So you end up with a hot pressurized container compared to the external environment. For small systems or long time storage, this means that heat will eventually leak out into the surrounding environment and you won't be able to get that heat energy back.
When you allow the gas to expand again to extract its energy, its temperature decreases. If there hasn't been enough time for a significant amount of the initial heat of compression to leak out of the system you can get nearly all your energy back (minus details like turbine and pump efficiencies) and the gas will come out at nearly the same temperature as it went in. If the heat of compression has leaked out, the gas will come out much colder than ambient temperature, which means that fittings and equipment will need to be able to handle cryogenic temperatures and ice build-up.
For large scale storage, you can often use tricks for storing the heat produced by compression in a material that can hold the heat for a long time which is highly insulated from the environment. Another way around heat energy losses is to continually exchange heat between the gas and its environment during the compression and expansion process in order to keep it the same temperature, although this method limits the power you can get to the power your heat exchanger can handle.
There is a limit to how much you can compress a gas. At about 700 atmospheres or so for simple molecules at room temperature, you have squished all the molecules together enough that they are nearly touching, at which point they stop behaving like a gas. Big complex molecules start touching at even lower pressures. This places an upper limit on how much compression you can get, beyond this you won't be storing very much additional energy by pressurizing it further.
The pressure vessel that contains the compressed gas has a specific energy that depends on the material limits of the stuff used to make it. But the gas itself also contributes to the mass of the storage, and can be significant when the material strength of the pressure vessel is high. For example, using the ideal gas law the mass of 1 m³ of hydrogen gas compressed to 700 atmospheres at room temperature is about 60 kg; any other gas will be more massive for the same compression. (In reality, hydrogen exhibits about 50% deviation from ideal gas properties at 700 atmospheres and room temperatures[10], but ideal gas behavior can at least get us in the ballpark for quick estimates.) This would require about 975 MJ to compress this gas without using fancy heat exchangers and allowing time for the gas to cool off. However, it will only store about 175 MJ of energy. From the material limits section, we can estimate that storing this compressed hydrogen would require about 700 kg of maraging steel, 60 kg of carbon fiber, or 4 kg of hypothetical perfect carbon nanotubes or similar materials. We can now immediately see that for advanced materials, the mass of the hydrogen dominates the mass of the system and using stronger materials does not significantly further decrease the mass.
Continuing this example further, releasing that hydrogen (again without using a heat exchanger) will allow you to extract 150 MJ at perfect efficiency. With no losses in the compressor and generator, you would get about 15% efficiency and would have a specific energy of approximately 2.4 MJ/kg if using ideal carbon super-materials for the gas canister. This is a bit better than a modern high-end Li-ion battery in terms of specific energy, but not by much; and the charge-discharge efficiency is much worse. Hydrogen is as good as you can possibly get for low mass compressed gas energy storage, if you use something like helium or nitrogen or air the performance will be worse. So compressed gas storage probably will not be used for compact energy storage in weight or mass limited applications like vehicles or zap gun energy packs. At least, not on its own - that same hydrogen run through a fuel cell might get you something like 4 GJ of energy back out! But for grid scale energy storage at lower pressures with tricks for storing heat or equalizing the heat during pumping compressed gas can start to look promising compared to other options.
Gravitational
Pushing a mass to a higher location is one way to store energy, when the mass is let back down it can deliver mechanical energy. In modern (2021) times, the main form of gravitational energy storage is pumped hydro – an impeller pumps water from a lower altitude source into a higher altitude reservoir. When the water is let back down, it can drive a turbine. There have been proposals for other gravitational energy storage devices like pulling a train full of rocks up a tall, steep mountain, or raising heavy concrete blocks up tall towers, but these have not yet been commonly implemented.
Thermal energy storage
A simple way to store energy is to heat up a medium to high temperatures, insulate that material, and then run a heat exchanger past it at a later time when you need to extract that heat. Molten salts and heat-insensitive oils are popular for this kind of storage, but even materials like sand and bricks have been used. Thermal energy storage is, for example, commonly used with solar-thermal energy plants, so that their hot sand or molten salts or heated oil can continue to boil water to run a turbine to generate electricity even after the sun has gone down.
When heat is the desired form of your energy, thermal energy storage looks even more promising. Many industrial processes require intense heat; district heating can make use of stored heat; and even solar rooftop water heaters can be used to cut down on household electricity bills.
Chemical energy storage
Energy stored in chemical form is usually called fuel. It includes things like gasoline, kerosene, and Diesel fuel, as well as natural gas (methane), ammonia, and hydrogen. In our modern (2021) world, most fuel is turned into useful work by burning it in a heat engine – producing heat from its combustion and using that heat to run through various thermodynamic cycles to extract part of it as work. However, some of them are used in fuel cells, that directly react the fuel to create electricity. Note that both of these methods introduce substantial inefficiencies into the process of using the energy – you won't be able to use the full energy of combustion released as heat that is reported here directly in your device.
Liquid hydrocarbons
Liquid hydrocarbons are things like gasoline, kerosene, and Diesel fuel. There are various and very important differences about what kind of engines they can burn in, but those are beyond the scope of this article. The main important thing is that burning 1 kg of liquid hydrocarbons in oxygen (such as that from the air) will produce about 45 MJ of heat.
Gaseous hydrocarbons
This includes things like methane, natural gas, and propane. They must be stored in pressurized bottles, often under enough pressure to turn the gas into a liquid for storage. When burned, methane produces about 55 MJ/kg of heat compared to the 50 MJ/kg of propane or butane, but the latter two are easier to store and transport.
Hydrogen
Hydrogen has the highest specific energy of any chemical fuel – about 120 MJ per kg of hydrogen burned. Unfortunately, hydrogen is also the hardest of these common fuels to store. In modern times (2021), in needs to be stored as a high pressure gas at very low density, or as a low density liquid that needs to be kept at cryogenic temperatures. However, there are research programs looking into hydrogen storage with the hydrogen adsorbed into chemical sponges or in the form of metal superhydrides that could potentially store hydrogen more safely and conveniently. Hydrogen is the easiest gas to burn in a fuel cell, and fuel cells are emerging as the preferred way to extract hydrogen energy for their efficiency, reliability, lack of emissions, and low maintenance.
Carbon
Carbon burns in air. But it's not all that great of a fuel. Complete combustion of pure carbon under ideal conditions can get you something like 33 MJ/kg of specific heat. But it's also a solid, so it is harder to work with in engines as granular material has much more, shall we say, interesting physics when it flows than liquids. And in our current conditions on Earth, it would also have the problem of contributing to the carbon dioxide load in the atmosphere, which is causing global climate problems. The only reason anyone would want to use it would be if they could just dig it up really cheaply from the ground.
It turns out, you can just dig it up really cheaply from the ground. This stuff's called coal. Even better, it's not pure carbon, so it can burn significantly easier. The problem is, it's not pure carbon. So it produces a lot of un-burnable toxic ash, chemicals that cause smog, acid rain, and tiny particulate aerosols that ruin people's lungs. In addition to the carbon dioxide greenhouse gases mentioned earlier. But while it has its downsides, it is a good resource for pulling yourself out of a pre-industrial level of development or producing electricity very cheaply (if you don't take into account all the costs to society once stuff leaves the smoke stack). Burning coal can generally give you something like 24 MJ/kg of coal fuel as heat.
Biomass
A lot of biological materials can be burned for heat and light. The list includes stuff from dried dung to whale oil. But the material that most people use for this, when they can, is wood. The energy content of wood varies somewhat depending on type, growth conditions, and all the other variabilities that can affect living things but generally hovers somewhere around 15 to 20 MJ of heat per kg of well dried wood fuel. Burning wood produces smoke that can cause respiratory problems and, if burned in large quantities, can lead to bad air quality. Wood ash is a good source of potash (a fertilizer) and in low-tech societies can be used to make soap.
If wood is heated in the absence of oxygen, it generates charcoal. Charcoal is primarily carbon (see above), but unlike coal lacks a lot of the toxic elements that make coal ash really nasty. Burning charcoal yields about 30 MJ of heat per kg of charcoal. In addition to burning charcoal for heat, it can also be used for materials processing (particularly for making steel in lower tech societies), filtration, a soil additive, a pigment for cosmetics or art, or as a component of making black powder.
There is occasionally interest in fermenting plants to produce alcohol for fuel (there is always interest in fermenting plants for reasons quite unrelated to fuel). Alcohol is not a great fuel – ethyl alcohol delivers 27 MJ of heat per kg of fuel – but it can be created in low tech situations where fossil fuels might not be available. In many cases, production of alcohol for fuel competes with food production which might discourage this use in many settings. In the 2000's there was a considerable flurry of research into making other kinds of fuel chemicals from quick-growing plants that did not compete with crop plants for land, such as furfural from switchgrass. In our world, not much came of this but an aspiring author might imagine a society where this research payed off.
One of the fastest growing sources of biomass is algae. If oil-rich strains of algae could be cheaply and reliably cultured in bulk, algae oil could become an important fuel. While research into this method was once promising, it has been plagued by problems and largely abandoned as of 2022.
Plant oils can be processed to produce biodiesel. This is a drop-in replacement for Diesel fuel produced from fossil fuels (see the section on liquid hydrocarbons).
High explosives
High explosives are sometimes considered when the need to extract energy quickly is more important than storing energy compactly. TNT releases about 4.2 MJ/kg of heat and work upon detonation, while more modern explosives like PETN release more like 6.7 MJ/kg. PETN is particularly interesting because very small diameters of the stuff can support a detonation wave, allowing it to be used in compact pulsed power applications that don't require a good fraction of a megajoule at a time. While this energy storage pales in comparison to that of hydrocarbons and hydrogen, it is convenient because modern high explosives are generally easy and safe to transport and store, and can release their energy in a very short period of time – with detonation speeds of around 7 to 8 km/s, high explosives will generally release all their energy in under a millisecond (with exceptions for things like very long strings of PETN det cord). High explosives are pretty hard on the motors and generators that use them as fuel, though – almost all are single use items.
Exotic chemistries
As the Galactic Library is dedicated to science fiction, it is worthwhile to look at a few chemistries that probably can't work. Some of them almost certainly can't work. But it is fun to imagine what might happen if they could.
Metastable helium
Helium is a very stable atom. Both of its electrons are snuggled up next to its nucleus in the lowest energy electron shell (or "orbital") with their spins opposite each other. It takes a lot of energy to bump one of the electrons up to the next highest level. If you do, the electron can quickly fall back down into the unoccupied orbital it left behind.
Except when it can't. The only option the electron has for giving up its energy to something else when falling back down is to give off a photon (a particle of light). Photons have specific "selection rules" that govern when they can be created. One of these is that the angular momentum of the orbital transition has to change by one quantum unit. The other is that the photon can't flip the spin of a particle. Both of the ground state electrons are in a state with no orbital angular momentum. So if you take one of them and bump it up to the next highest orbital with no orbital angular momentum, and if you flip its spin in the process, you get it to a state where there are no easy ways to actually give up its energy. If there were an intermediate energy state between this excited state and the ground state, maybe it could decay to the intermediate state and then to the ground state, but there is no such state in the helium atom. That electron could be stuck there forever! This is called metastable helium, and it actually exists.
Of course, it won't actually be stuck there forever. First, there are always higher-order processes that can occur that allow some kind of decay. So an isolated metastable helium atom lives for only about 2 hours before emitting some ultraviolet light and returning to the ground state.
Secondly, if the metastable helium atom bumps into some other atom or molecule, the excited electron can grab hold of an electron on the thing it bumps into, rip it off, and throw it away; giving that ejected electron the extra energy needed for the original excited electron to fall back where it belongs. So you need to keep it isolated.
But, if you could find some way to stabilize this state and store it in bulk, it would release nearly 500 MJ/kg when made to return to its ground state.
Core chemistry
When electrons are attached to atoms, they arrange themselves in various states or "orbitals" with well defined energy levels. Generally, you can put a certain number of electrons into orbitals with similar energies, called an "electron shell", before the shell gets filled up and you need to start putting electrons at higher energies. The outermost, usually partially filled, shell, at the highest energy, is called the "valence level", while all the filled inner shells are called "cores".
When two atoms with partially filled valence shells meet, it is energetically favorable for them to share electrons between them so that together they can get closer to a filled valence shell. This is called a chemical bond.
So what happens if we knock an electrons out of a core level of two atoms, strip off the valence electrons, and bring the two atoms together? They should form a chemical bond by sharing their core electrons. This core bond, made with more tightly bound and energetic core electrons, should be much stronger and store much more energy than the normal chemical bonds made by valence electrons.
Now there are a lot of problems with this idea. For one thing, those two atoms need to be highly charged to do this, so they will attract other electrons back to them. While these may initially find a home in the valence shell, it is energetically favorable for any valence electron to fall down into the empty core orbital which would break the core bond. So under normal conditions these core bonds won't last for long. But maybe you could find a system where the core bond is metastable? Where it takes a significant extra kick to get the valence electrons to take up their rightful place back in the core? Where core bonds could last indefinitely in bulk material?
If you could do such a thing, your core bonded material would be an extremely dense, extremely strong substance. And it could release a lot of energy when it chemically reacted with anything in such a way as to affect its core bonds. It would release an order of magnitude more energy than normal chemical reactions from just shallow cores. And if you could somehow make this work for the inner cores of heavy atoms, you could increase the energy release by maybe up to three or four orders of magnitude.
Keep in mind, that this speculation almost certainly won't actually work (although it hasn't been entirely ruled out – it's hard to prove a negative). But for science fiction, it makes a not-too-unreasonable handwave to justify super-strong materials, super-dense materials, and compact energy storage. It would also explain why everything seems to be made out of explodium, erupting in massive fireballs when hit by blaster fire or bullets like we see in so many popular franchises – the metastable nature of core bonded materials would make them fail very catastrophically if they were disturbed too much.
Nuclear energy storage
The strong nuclear force that binds together atomic nuclei is many orders of magnitude more potent than the electromagnetic force that makes chemical bonds and holds molecules and physical structures together. Consequently, atomic nuclei can store far more energy than any chemical fuel, mechanical device, or electro-chemical cell. However, there are a number of significant challenges involved with storing energy in nuclear interactions.
Energetic nuclear states are difficult to make. In most cases, these are not something that can be "charged up" at home and then used in the field. You rely on energy that has been stored for billions of years by processes far beyond the human scale – the deaths of giant stars, or the very formation of the universe. As such, this stored nuclear energy is more of a natural resource to be extracted from the environment. There are exceptions to this, which we will cover.
The nuclear reactions that liberate the nuclear energy invariably emit nuclear radiation - that is how the nuclear energy is emitted after all. Consequently, any nuclear energy storage will involve radiation hazards. Depending on the method used these can be minimized or mitigated with proper procedures and design, but it will always be a factor to consider.
Radioactive isotopes
The simplest way to transport and extract nuclear energy is to use radioactive isotopes. These decay at a constant rate relative to their current quantity, releasing radiation that can be turned into heat. This heat can then be used to run a heat engine, perhaps a Stirling engine or a thermocouple.
Ideally, you would choose an isotope with a long enough half-life to give adequate power for the duration of the mission or device lifetime. But you don't want the half-life to be too long, or the specific power produced will be low. In addition, an isotope that decays without any gamma rays from its immediate decay or later down its decay chain will make shielding much easier – your main radiological concern will then be containment of the radioactive material to avoid contamination rather than shielding. The isotope 238Pu is nearly ideal for many applications – its 88 year half life gives a long enough device lifetime while providing high specific power, and it emits negligible gamma rays from its decay. Note that 238Pu is a non-fissile isotope of plutonium, and is thus useless for bombs and reactors.
An alternate method of capturing energy from radioactive decay is with betavoltaic materials. Sandwiching thin layers of a beta emitter between semiconductor layers with p-n junctions similar to those used by photovoltaic panels can capture the energy of the ionization created by the beta particles. Betavoltaics are currently at a very early stage of development, and it is impossible to know how they will pan out. For fictional purposes it would be reasonable to assume that you could use them to make long-lived nuclear batteries. Speculatively, such devices might capture something like 10% of the decay energy of isotopes such as tritium or 14C, neither of which emit gamma rays while decaying.
Some proposals have even suggested using the radiation produced by radioisotopes to make scintillator materials glow, and then capturing that light with photovoltaic cells to produce electricity.
Radioactive isotopes are one of the nuclear methods we have for actually storing energy created by other processes. The isotopes can be directly created by irradiation of inert material or nuclear fuel in a reactor, or by using grid electricity to run a particle accelerator. This storage is not efficient, but it is technically storage of generated energy.
As far as nuclear energy storage goes, radioisotopes are not particularly energy dense, they have the disadvantage that they cannot be turned off, and have relatively poor efficiency at turning released heat into usable energy. If your setting includes some ultra-tech handwavy method of inducing or artificially stabilizing nuclear decay, then radioactive isotopes might become significantly more attractive for energy storage and production. We currently have no idea how you would go about doing this, but this is science fiction so go ahead and try it in your setting! Off the wall ideas for doing so could include the quantum Zeno effect (decohere the nuclear state fast enough with quantum "observations" that it can't ever change). Or maybe an isotope that decays primarily by electron capture – fully ionize it and it has no electrons to capture any longer, leaving only the (potentially much slower) beta+ decay branch. You can turn on the decay again by giving it its electrons back.
Nuclear isomer
An isomer is a certain configuration of protons and neutrons in a nucleus. Different isomers of the same isotope will have different energies. Isomers with higher energies will decay into lower energy isomers via gamma radiation or internal conversion. In this sense, isomers with energies higher than the ground state are radioactive isotopes, and to a large extent they can be handled as in the above section except that, because they decay specifically by emitting gamma rays, no one would want to use them.
The reason nuclear isomers are singled out was that for a brief moment, people though that maybe you could trigger the decay of a particular isomer 178m2Hf through stimulated emission (the same thing that makes lasers work). In particular, this old-time German physicist named Albert Einstein (perhaps you've heard of him?) did some math and showed that in order for statistical mechanics to make any sense, physics required that a system in an excited state capable of emitting electromagnetic radiation to decay to a lower energy state could be triggered to emit that radiation if it was hit by that exact frequency of radiation that could be emitted by that transition. This new radiation would be in phase with the triggering radiation, going in the same direction with the same polarization and having all other identifying features the same. So yeah, in addition to formulating both of the mind-bending theories of special and general relativity, in addition to kick-starting quantum mechanics by explaining the photo-electric effect, in addition to finally proving the existence of atoms once and for all by explaining Brownian motion, he also predicted lasers by some fourty years before the first one was ever demonstrated. But I digress …
So, you should be able to stimulate gamma decay by hitting an excited isomer with a gamma ray of the same energy that it emits. or actually, of a slightly greater energy than it emits, because so far our discussion has neglected an important detail – nuclear recoil. When an isomer decays, the departing gamma ray has some momentum, so to conserve momentum the nucleus gets kicked in the opposite direction. This gives the nucleus kinetic energy, which must also come from the energy from the isomeric transition. So it turns out that the gamma ray only gets most of the energy, not all of it. And this is why radioactive isomer samples don't undergo spontaneous lasing to produce deadly beams of gamma rays while discharging all of their radioactivity.
Except – there is this odd effect in physics called the Mössbauer effect, where a radioactive material decaying in a solid will sometimes not recoil at all. This allows it to participate in stimulated emission from others of its kind. If you could get the right kind of isomer in the right kind of crystal that enhanced this Mössbauer effect enough, maybe you could make a gamma ray laser!
In addition to stimulated emission, it is conceptually possible that gamma emission could be triggered in an isomer through some other process, such as bombardment with other forms of radiation. If the decay of a bulk sample of the 178m2Hf isomer could be triggered, it would release a specific energy of about 1.3 GJ/g, or 300 kg of TNT equivalent per gram of isomer.
it is with this background, that one can see the interest that was generated when research in the late 1990's suggested that 178m2Hf could be triggered. This sparked a flurry of research which, unfortunately, mostly showed by the early 2000's that nothing of the sort actually occurred. This is, of course, how science is supposed to work with independent checking by other groups to make sure that inconsistent and spurious results are weeded out. But it would be interesting to consider what would happen if you could trigger gamma decay at will.
Fission
A fission reactor liberates energy stored by ancient dying stars. It produces copious amounts of neutron and gamma radiation as well as highly radioactive isotopes and long-lived radioactive isotopes in its fuel, cladding, coolant, and containment structure. However, it also produces high amounts of heat on demand that can either be used directly or to run a heat engine to efficiently produce electricity. Fission reactors can be made small, such as the paper-towel-roll-attached-to-a-patio-umbrella sized kilopower[11]. However, fission reactors generally benefit from large scale installations; in particular shielding becomes relatively less of an issue as the installation becomes bigger.
The complete fission of a kilogram of nuclear fuel would release something like 80 TJ. However, reactor designs in modern (2025) use can't achieve this because of the buildup of neutron absorbing fission products (the so called "neutron poisons"), and because nuclear fuel usually only has a small fraction of the fissile stuff (in commercial reactor fuel, about 3% to 5% of the uranium is the fissile 235U while the rest is 238U which doesn't fission when hit by thermal neutrons. In addition, the uranium is chemically bound to oxygen to make uranium oxide pellets, which are then held inside long fuel pins made of zircaloy metal and bundled into a fuel assembly held together with more zircaloy. Although the full energy picture is complicated because while the thermal neutrons can't fission 238U, they can transmute it into 239Pu which is fissile and the fast neutrons direct from fission, before they have a chance to slow down, have a small chance of causing some 238U fission. Look, nuclear engineering is complicated stuff, okay? It's why people have to go to college to learn this kind of stuff). A more realistic estimate of the specific energy of modern nuclear fuel is a reasonable fraction of a TJ/kg. Reprocessing fuel removes the poisons from spent fuel, allowing more of the fuel to be used. Some proposed designs, such as the molten salt reactors, use on-line reprocessing to allow full burnup without an extra facility. (Molten salt reactors are also appealing in that they would allow greatly reduced volume of radioactive waste as well as the complete elimination of the very long lived radioactive waste, which is simply burned as fuel.)
Fusion
A fusion reactor is a still hypothetical concept for generating power (as of 2022). Although fusion has been demonstrated in a laboratory, it is still a long way from practical applications. Still, for science fiction is is often popular to assume that fusion can be harnessed to create net energy. This uses the stored energy of light isotopes left over from the creation of the universe. A fusion reactor would produce even more radiation than a fission reactor, as well as copious amounts of high activity isotopes from neutron activation. It does have the benefit that the radioactive material it produces would be shorter lived than that of a fission reactor, with secure storage and isolation only required for years or decades instead of longer than all of current human civilization. Fusion reactors benefit greatly from being built at large scale. It is likely that the minimum viable size for a fusion reactor is something that takes up a large warehouse, if not a modest skyscraper. The most practical form of fusion (fusing the hydrogen isotopes deuterium and tritium) would use its intense neutron flux to heat a working fluid (likely lithium to allow it to regenerate its radioactive fuel) which would then run a heat engine.
The most practical kind of fusion to get going is the fusion of deuterium with tritium. This process has a specific energy of 340 TJ/kg, although some designs (such as intertial confinement fusion) will reduce the specific energy of the stuff you have to carry around by enclosing the fusion fuel in cladding. There is also the complication that tritium is radioactive, with a 12-year half-life. So it is often proposed for fusion reactors to generate their own tritium on-line by letting the neutrons from fusion enter a blanket of lithium around the reactor, which will transmute some of the lithium to tritium. If you are considering the deuterium and lithium as the fuel, the specific energy is more like 210 TJ/kg.
Other reactor fuels are much harder to ignite. But among the plausible ones, fusing deuterium with itself would give 350 TJ/kg (assuming that the tritium and helium-3 reaction products also react with the deuterium), and deuterium fusing with helium-3 would also yield about 350 TJ/kg. If we go somewhat lower in plausibility, the fusion of hydrogen with boron-11 is probably impossible to ignite (it always loses more energy to bremsstrahlung x-rays than it gains by fusion reactions) but if you assume it is possible you could get out 70 TJ/kg.
This page would not be complete without noting that there is, in fact, one working fusion reactor that has been producing net power for some time. Specifically, for 4.6 billion years. And it is expected to continue producing power for another four and a half billion year or so. It is located about 150 million kilometers away from our planet, and puts out an astounding 380 trillion TW. Unfortunately, it has a mass of more than 330,000 times that of our entire planet, so it is not easily portable. This is, of course, our sun. We can directly capture its light for electricity production using photovoltaic panels, or concentrating mirrors to run heat engines. Plants use its light to produce energetic chemicals for fuel. Burning gasoline or coal uses energy from sunlight captured long ago. So in some sense, nearly all the energy we have ever used on our planet, across all of human civilization, comes from fusion.
And with that, we can continue our discussion of various fusion fuels. And, unfortunately, pop a few bubbles. Because one of the more popular fusion fuels used in science fiction is the fusion of protons (normal hydrogen) directly into helium. This is what the sun does, after all. And hydrogen is very common in our universe, so it is easy to get a hold of. However, note that our sun has lasted for about four and a half billion years, and will probably last for another four and a half billion years. This means that even with the conditions in the core of a sun, it takes nine billion years to burn up protons as nuclear fuel. This is an awful long time to wait to get your energy out! And this is reflected in the abysmal specific powers of suns – note from the power and mass we discussed for our sun that its specific power is a miserable 0.2 milliwatts per kilogram! The resting metabolism of a human is about 1 watt per kilogram. That's right, you are about five thousand times more power dense than the sun! If you can get to temperatures and pressures even more extreme than that inside our sun, the fusion can go a bit faster. This can be accomplished by using nuclear catalysis like the CNO cycle, for example. But even under the conditions of the most extreme stars of our universe it takes something like ten million years to burn their fuel. And under stellar core conditions, the plasma will be radiating far more energy away as x-rays than it is producing as fusion, so that unless you have a star's worth of insulation around your fusing plasma you will use up more energy than you make trying to get it to fuse. So realistically, proton-proton fusion is probably off the table outside of stars.
Exotic nuclear matter
There are some interesting informed speculations out there for exotic ways that nuclear matter can arrange itself. Because nuclear matter has such a large energy difference compared to chemical matter, those which are stable at low pressure (meaning they can exist outside of the crushing gravity of a neutron star) are interesting candidates for storing energy.
One of these possibilities is strange matter. We know of six kinds of quark that can exist, but as far as we know only two of these are stable: the up quark and the down quark. Different combinations of up quark and down quark make up the neutron and the proton (the proton is up-up-down, the neutron is up-down-down). As far as we know, all other kinds of quarks only exist fleetingly as the temporary debris of high energy particle collisions. These other exotic quarks are much more massive than the normal up and down quarks that make up everyday matter, meaning they have a lot of extra energy, and will invariably quickly decay to an up or down quark and various other particles needed to conserve energy and momentum and various particle physics stuff like lepton number.
But if you get a large enough nucleus, something strange can happen. Two up quarks can't be in the same quantum state. Nor can two down quarks. If you pack more quarks (via their collections of three into protons and neutrons) into a nucleus, the newer quarks are forced to occupy higher and higher energy levels. But an exotic quark in the nucleus could hang out in a low energy level. If the energy levels available for new up and down quarks is high enough, it becomes energetically favorable for the up or down quarks to decay into exotic quarks – exotic quarks which cannot then decay, because there is no quantum state in which they can put the up or down quark they would decay into with the energy they have available from their decay. So the stable state of really big nuclei might have equal numbers of up, down, and exotic quarks.
The lightest exotic quark is called the strange quark. This is the quark that is most likely to form nuclear matter with exotic quarks. So nuclear matter made up of a mix of up, down, and strange quarks is called strange matter and isolated clumps of it are called strangelets. Large atomic nuclei are unstable because they have a large electric charge, so when they get big enough their electric self-repulsion overcomes any nuclear forces sticking them together and the nucleus falls apart via fission. But a strangelet with equal numbers up, down, and strange quarks would have zero electric charge. There is no limit to how big a strangelet could get.
A strangelet would be a form of nuclear matter. Thus it would be as dense as nuclear matter, on the order of 1018 kg/m3.
If you had a strangelet, you could get energy by shooting atomic nuclei into it. Those nuclei would stick, and then some of their ordinary quarks would decay into strange quarks. The strangelet would absorb any normal nuclear matter it encounters, turning it into more strange matter. The exact energetics are not known, but again as a form of nuclear matter it could be expected to liberate something on the order of 1014 J/kg (tens of kilotons TNT equivalent per kg). If your strangelet starts getting too big and heavy, you might be able to "recharge" it by shooting it with a particle beam to knock pieces off of it.
Strangelets will probably have a slight excess of up and down quarks, giving them an overall positive electric charge. This complicates feeding them with atomic nuclei, which also have a positive charge. You run into many of the same problems you have with nuclear fusion, which has much the same problem. But for all the headaches this might give us for using strangelets for making energy, it is actually a very good thing. If the strangelet were neutral, or worse, negatively charged, there would be nothing preventing a runaway reaction where it just keeps absorbing all matter in its vicinity, turning everything into strange matter. A single negatively charged strangelet dropped onto a planet would destroy the planet, eating all of its matter in a continuous, ever-growing nuclear fireball and eventually leaving a planet-mass strangelet in its place. So in this case, be thankful for the difficulties involved!
Nuclear Catalysis
A catalyst is a chemical which speeds up a chemical reaction without itself being consumed by the reaction. Could there be an analogue for nuclear reactions? Some sort of particle that increases the rate at which nuclear reactions occur without being damaged in the process?
There are a couple ideas on how to do this. One of the best known, and with the strongest theoretical foundation, is muon catalyzed fusion. A muon is a particle that basically acts like a heavy electron or positron. A muon with a negative charge can be captured by a nucleus just like electrons are, but because the muon is 207 times heavier than an electron, it will be 207 times closer to the nucleus, on average, than the electron would be. Also, the negative charge of the muon will screen the positive charge of the nucleus to anything farther away from the nucleus than the muon, making it seem as if the nucleus has a lower overall charge. If the nucleus in question is deuterium that only has a single positive charge the muon - deuterium combo will look electrically neutral. This will let a muonic deuterium atom get 207 times closer to other deuterium atoms than normal electronic atoms would. This is close enough that nuclear fusion can take place. When the fusion reaction kicks the muon back out into the deuterium, it can continue to cause more fusions, thus acting like a proper catalyst. Irradiating deuterium with muons does indeed cause some fusion to occur.
Unfortunately, there are a couple of issues with this. The first is that muons are unstable. They decay into an electron and a couple of neutrinos within a couple of microseconds. While the muons do cause some fusions, they do not make enough to liberate sufficient fusion energy to pay for the energy cost of making the muons themselves. The other issue is that when the muon causes fusion, they might continue to stick to the fused nucleus. If the fused nucleus is still reactive (like tritium or 3He you get from deuterium fusion) it can continue to go on to produce more fusions with the deuterium. However, if it is not very reactive (like the 4He you get from fusing that tritium or 3He with deuterium) then this removes the muon from the system and shuts down any further fusion.
Another potential nuclear catalyst are magnetic monopoles. These monopoles are hypothetical particles that are predicted by some theories. While they have a strong theoretical foundation, none have ever been conclusively observed[12]. However, if they exist, they are expected to react with some nuclei. Some nuclei are magnetic, and a magnetic nucleus can bind to a magnetic monopole. The nucleus with a bound monopole can then undergo various reactions[13].
For example, if you put a monopole into 3He, it can bind to a 3He nucleus. The magnetic attraction can then attract other 3He nuclei. This magnetic attraction lowers the repulsion keeping them apart by their nuclear charge. It is likely (but not certain) that this could increase the rate at which 3He undergoes fusion with itself to something usable for energy generation. Because 3He - 3He fusion is truly aneutronic, this would provide one route to low-radiation nuclear energy.
A monopole's magnetic field can pull on the magnetic orientations of the individual protons and neutrons in a nucleus to make it more energetically favorable to align them with the monopole's field. This would favor nuclei re-arranging to a higher magnetic moment when close to a monopole. This mixing of the nuclear states could act as a catalyst for some nuclear decays. This could allow a radioactive isotope generator that could be turned on and off, which would make it much more useful and versatile. The monopole could also encourage spontaneous fission – a kind of radioactive decay when a heavy fissionable nucleus splits apart without being triggered by an external photon or neutron. This could allow a monopole-controlled fission reactor that could not undergo meltdown.
Compressed matter
We have previously talked about compressing springs and gases. But these discussions had been bounded by the realms of the possible. The maximum pressure that can be sustained by materials held together by chemical bonds will be not too far from what can be sustained by atomically perfect graphene. If you could somehow apply a uniform layer of such graphene in uniform tension around a sphere, you could keep a pressure of around 130 GPa. The only known way to obtain pressures much higher than that are dynamically (such in collisions, or with high energy releases such as a detonating nuclear explosive) or gravitationally with the matter bound together by the mass of a planet or star. While such situations might be impractical, they can be fun to consider.
Metallic hydrogen
Hydrogen under extreme pressure (several hundred GPa at least) is believed to enter a metallic state. There has been some speculation that this metallic hydrogen might be metastable – that is, if you release the pressure it would remain a metal. Such a material would likely be of very low density compared to other metals, and may be a room temperature superconductor. When it decomposed into normal hydrogen, it is expected it would release on the order of 100 MJ/kg, which could be extracted, for instance, by running the resulting hydrogen exhaust gas through a turbine. Unfortunately, there is no evidence that metallic hydrogen is metastable.
Electron degenerate matter
No two electrons can occupy the same quantum state. This can be expressed as no two electrons (with the same spin) can occupy the same place at the same time, but an equivalent statement is that you can't have more than one electron (with the same spin) in a given electron energy level. As you compress matter, you are trying to compress more and more electrons into the same number of available energy levels. Eventually you reach a state called a degenerate Fermi gas, where all the low-lying electron states are filled, and to cram in more electrons you need to put them in higher and higher energy states on top of the ones already filled. When a star runs out of fusion fuel, cools off, and contracts, it will get crushed under its own gravity to an electron degenerate state with densities on the order of a billion kilograms per cubic meter (109 kg/m3). Under these conditions, the degenerate electron gas will have a specific energy on the order of a kiloton per kilogram and a pressure of around 3×1021 Pa (30,000 trillion times Earth atmospheric pressure).
Note that the electron degenerate gas is unbound. There is nothing keeping it together other than whatever is supplying the external pressure (usually the gravity of a dead sun). If removed from that pressure it will immediately expand. Violently. Immediately liberating that kiloton per kg in a massive explosion. There is no material that can contain those pressures – and even if there was, the most energetic electrons in the degenerate matter at that density are flying around at energies typical of radioactive beta decay (about 150 keV, for the density discussed here), fast enough to simply ignore chemical bonds and go shooting through matter unhindered, except for the trail of ionization destruction that they would leave in their wake. So comparisons you often find like "one teaspoon of white dwarf material would weigh as much as a freight train" gloss over the fact that you simply can't take that teaspoon away from the white dwarf – such things are simply inconsistent with existence under conditions typical of Earth (or outer space, or the even core of an active sun).
But if you have Sufficiently Advanced aliens in your setting, with access to non-molecular supermaterials or force screens or something; and if those are sufficient to contain electron degenerate matter, now you have some idea of what it would do.
Neutronium
Once the energies of the fastest electrons in electron degenerate matter get to be more than about an MeV, they can react with any protons that happen to be lying around to make a neutron (and also an electron neutrino, but that has no real consequences to what we're talking about). These neutrons will be unable to decay, because there is no available energy states for their decay electrons to go into that can be reached with their decay energy. This puts a cap on the electron degeneracy, any denser just starts turning protons into neutrons.
These neutrons can then be compressed to a neutron degenerate state. In science fiction, this is commonly called neutronium. This is like an electron degenerate state, only much more extreme. It is four hundred million times denser, under 0.4 trillion times more pressure, and has a specific energy of around a megaton per kilogram.
Like electron degenerate matter, neutronium is not bound. There is nothing keeping the neutrons stuck together except for the crushing gravity of the neutron star. Removed from that, they explode outward violently, with an energy spectrum ranging up to 70 MeV at the upper end. These are very high energy neutrons, with all of the issues of normal neutron radiation (ionizing radiation dose, activation, embrittlement, triggering fission, being radioactive, etc.). And note that those 70 MeV neutrons are not being made during the explosion or boosted up to 70 MeV or anything. They were always there, with their 70 MeV of energy, but just couldn't get out. And now they can.
Again, if there are Sufficiently Advanced civilizations with the means to confine neutronium, now you know what it is capable of.
Matter storage
Most forms of energy storage make use of matter for structure, coolant, flow control, conducting electricity, and so on. However, matter itself contains very large amounts of energy. Every kilogram of matter holds within it 9,000 terajoules of energy. Unfortunately, it seems to be incredibly difficult to get that energy out. Further, any ways of extracting that energy from matter look to involve getting that energy as copious amounts of energetic radiation, which will require extensive shielding, precautions to prevent the spread of radioactive material, and radiation damage to the operating structure.
Antimatter
The method of energy extraction from matter with the best theoretical footing is the use of antimatter. When antimatter meets matter, they annihilate, releasing the total energy bound up in the mass of the annihilation reactants as various forms of energetic radiation – primarily pions and gamma rays. When an anti-proton or anti-neutron reacts with a nucleus of matter with more than one proton or neutron, one proton or neutron will annihilate and some of the annihilation energy is likely to go into shattering the nucleus, producing a shower of nuclear fragments ranging from isolated protons and neutrons to various light or medium ions. This in turn will create copious amounts of neutron radiation as well (along with more gamma rays). If the anti-proton or anti-neutron was also part of an antimatter nucleus, you will get antimatter nuclear fragments including copious anti-neutron radiation as well. So while antimatter-matter annihilation can provide very energy dense storage, it also produces a very severe high radiation environment that is hostile not only to life but also to materials (from the pions and anti-neutrons disintegrating nuclei, neutrons transmuting nuclei and disordering the atomic structures, and very high energy gamma rays inducing photo-nuclear interactions to break up nuclei).
One of the central tenets of engineering is to make things fail safe. That is, in the event of a failure, the engineered device should enter a safe mode that does not cause further harm. Antimatter must be kept isolated from normal matter in high vacuum in containers that use electric and magnetic fields to keep the antimatter away from the walls. This is inherently fail-dangerous. Perhaps in space, there might be ways to ensure that a containment failure will simply eject the antimatter into vacuum. But in any other environment, containment failure will result in uncontrolled annihilation and the sudden release of all stored energy.
Antimatter containment must be kept under high vacuum. No vacuum is perfect. There is always some sort of outgassing or sublimation or leakage. This can be minimized, and the continual operation of pumps can keep the interior gas density very low, but there will be some gas present. And this gas will react with the antimatter. So the simple act of storage leads to a significant radiation hazard. And if the pumps fail or you lose power to the pumps, you get a quickly rising amount of radiation that will heat up the containment or cause sputtering from the surfaces, causing additional leakage and outgassing, leading to more annihilation in a runaway process that ends in runaway containment failure.
The antimatter containment system required to separate the antimatter from the surrounding matter will not be small, requiring vacuum vessels, vacuum pumps, electromagnets, high voltage systems, sensors and active control systems, and probably a lot more. This significantly cuts into the specific energy of the system. So you won't get that theoretical 9,000 TJ/kg. Often by a great many orders of magnitude, although some proposals[14] for levitating solid anti lithium hydride might just cut into the specific energy by a couple orders of magnitude. For storage in the hard vacuum of outer space, you might perhaps even approach the theoretical limit.
Unfortunately, other than the occasional short-lived product of a cosmic ray collision, antimatter does not occur naturally in nature. This can make it a challenge to obtain.
For the speculatively minded, one possibility may be to make the antimatter on the fly from normal matter. There are various obscure possibilities for this in particle physics and general relativity, but none with any experimental foundation. Still, if you want to minimize unfounded assumptions in your galaxy spanning setting, you might use wormholes both for your travel and to create antimatter (as non-orientable wormholes).
But what if you don't have one of these matter-to-antimatter converters on hand? Don't despair, there are ways you can make antimatter from scratch. Particle accelerators can collide particles with each other with sufficient violence to create matter-antimatter pairs. If the antimatter is collected, you can gather antimatter fuel for the price of just electricity[14]. It may be possible to get efficiencies as high as 1% for turning electricity into stored antimatter annihilation energy (taking the mass-energy of both the antimatter and whatever matter it reacts with into account)[15]. Such methods might be able to supply on the order of tens of grams of antimatter, suitable for some interstellar expeditions.
There have even been proposals to mine the antimatter that does get produced by cosmic ray collisions with the upper atmosphere or other nearby planetary material (such as ring systems), and which becomes trapped in planetary magnetic fields outside of the atmosphere[16]. The amount is not large – Earth is estimated to hold a total of 160 ng of antimatter trapped in its magnetic field, which refills at a rate of 2 ng/year. The best place in our solar system for antimatter is thought to be Saturn, with 10 μg trapped and a production rate of 240 μg/year.
Baryon decay
As far as we have been able to observe, protons are absolutely stable. Neutrons outside of nuclei are unstable, decaying into protons in about 15 minutes. Cozied up inside of a nucleus, however, neutrons can be absolutely stable as well. Neutrons and protons are the two lightest baryons (the so-called nucleons, because they make up the atomic nucleus), and are the only baryons to be found naturally except for the ephemeral results of cosmic ray collisions or, potentially, inside the hearts of neutron stars.
However, there are some theoretical methods to get these stable baryons to split apart, liberating their energy in a hellfire of radiation. You usually require some exotic conditions, perhaps a remnant of the primordial vacuum from the earliest universe, which allows the baryon to turn into one or more mesons and a lepton (such as an electron, positron, or neutrino), all of which are very fast moving and energetic.
One such possibility is a GUT monopole[17]. This is a relic of the early universe where some bit of the primordial vacuum is preserved in a knot of twisting fields that can't smooth out, resulting in a net isolated magnetic pole. These hypothetical particles are predicted to exist, but have never been observed (although there are good explanations as to why they may be rare). Monopoles capable of causing baryon decay are likely to have a mass of between a hundred thousand trillion and a million trillion (1017 — 1018) times the mass of a proton.
The magnetic fields of a monopole would be repelled from diamagnetic materials and attracted to paramagnetic and ferromagnetic materials. This could allow monopoles to be caught in materials such as iron. The core electrons of all atoms are diamagnetic, so magnetic monopoles would be repelled from the inner core electrons before they can hit the nucleus (or, because of their relative mass, it might be more accurate to say that the atoms would be repelled from the monopoles). To start the baryon decay process and begin liberating that matter energy, you will either need to ram the atoms into the monopole hard enough to overcome their mutual repulsion, or you will need to completely ionize the atom to a bare nucleus and free electrons, allowing the atom to approach the monopole unhindered. In this way, monopoles can be stored safely until it is time to use them.
If a monopole encounters a nucleus consisting of more than just one nucleon, the meson(s) created by the decay of the impacted nucleon is likely to hit the rest of the nucleus, releasing its energy by shattering the nucleus into bits. This will produce radioactive debris and radiation in the form of neutrons and gamma rays.
A magnetic monopole is a zero-dimensional topological defect in the vacuum state of the universe. Other relic topological defects in the fabric of creation include cosmic strings (1-dimensional) and domain walls (2-dimensional). These are both also expected to catalyze baryon decay, but both are extremely heavy, such that they are unlikely to be practical for transport – or even for safely keeping on a planet.
Sphalerons are hypothetical unstable particle-like disturbances in the vacuum resulting from electroweak symmetry breaking. Like monopoles, they are predicted to allow baryon decay. Sphalerons processes become significant at temperatures of about 100 GeV; 100 times larger than the proton energy. This poses an issue: if the temperature is over 100 times the proton's rest mass then each proton will have a kinetic energy on the order of 300 times more than will be liberated by burning that proton with a sphaleron. You will need to be able to harness the energy of the 100 GeV plasma with an efficiency of more than 99.67% in order to get out more useful work than the energy you put in. For example, radiation increases sharply with increasing temperature, and an electroweak-hot plasma will be exceedingly hot. Radiation losses will be considerable, and you will need to ensure that the rate of sphaleron burning of protons exceeds the emission of radiation by more than a factor of 300 – and this is before taking into account inefficiencies in collecting the energy of the hot plasma after the burning process is complete.
Accretion disks
If you drop matter at a black hole but somewhat offset from a direct line, conservation of angular momentum dictates that the stuff dropped will start to orbit around the black hole instead of falling straight through the event horizon. As the matter approaches the hole, those parts of the object that are closer will experience higher gravity than those farther away, making them orbit faster. These tidal forces rip the object apart, spreading it out into a disk around the hole, and the way that the tidal forces squeeze and shear this material heat the matter up. As the matter gets hot, it radiates away some of that heat, causing it to lose energy and fall closer in to the hole, which in turn generates more heat. This process will convert about 40% of the mass energy of an infalling object into radiation. Although less efficient than antimatter or baryon decay, it has the advantage that a lot of the emitted energy is easier to use – infrared to x-rays rather than high energy gamma rays and exotic penetrating particles. It has the disadvantage of requiring a black hole.
Space-time storage
Black hole creation
if moderate amounts of matter or energy can somehow be crushed into a black hole, that black hole will almost instantly evaporate via the Hawking process to produce a flash of electromagnetic radiation. The fact that no one can figure out any way to cause such a collapse is a bit of a hitch in this plan, but we can speculate on the results of what would happen if you did so.
A small black hole cannot be fed. Its radiation produces so much pressure than incoming matter is pushed away from the hole, and even without that matter bunches up in a jam trying to get into the tiny hole so that it can only feed at a trickle. So such a hole is in some sense "safe" – you made it, it can't eat the planet, and no matter what you do it is going to evaporate in a flash of energetic radiation. The minimum mass at which a black hole can start eating material is a bit under 100 million metric tons; but not until approximately 100 million tons can it absorb matter faster than it radiates away the energy it is getting. So if you keep your hole at significantly less than 100 million tons, you won't be endangering the planet. And just for reference, that 100 million ton black hole will be spitting out a variety of 100 MeV radiation particles (gamma rays, neutrinos, electron, positrons, muons, various mesons, and gravitational waves) at a rate of 1.4 TW (of which about 700 GW of which is capable of interacting with matter), with a lifetime (if it doesn't eat anything) of about 67 million years. If it is allowed to eat stuff, it will stabilize to a power output of around 1.25 TW between its hawking radiation and the radiation from its accretion disk. And that 100 million tons will be compactified into a radius five times smaller than a proton, so there is no way that you can actually hold on to it in any kind of gravitational field – it will simply fall into the planet with little resistance, eating a few micrograms of stuff each second and putting out as much power as a large power station as harsh radiation as it plunges into the Earth.
But what about a smaller hole. Like, one that is formed from only a kg of matter. Such a hole will completely evaporate in less than one ten-thousandth of a trillionth of a second, releasing on the order of 20 megatons of energy in the process in the form of extremely high energy particles; gamma rays and hadrons and leptons of all kinds, weak vector bosons, Higgs particles, and perhaps other exotic paticles we haven't detected yet, all at energies so high that we don't really know how they would behave because we lack any experimental evidence at that energy scale, but which would probably produce extensive hadronic and gamma air showers scattering intense radiation over many kilometers in all directions. But at least anyone affected by the radiation will also have been burned to a crisp by the thermal flash before being blow to crumbly bits by the blast wave.
To get a hole that lasts for one second, it needs to be a bit over 1000 tons (with a yield of 25 trillion tons TNT equivalent) and will emit 10 TeV particles as its radiation. Holes that produce less than a megaton of yield will produce even more energetic and exotic radiation that the 1 kg variety, that will be likely to pose a radiation threat to the entire area. So black hole power sources seem to be a bit finicky to use.
Penrose process
If a black hole is spinning, you get an effect vaguely like a space-time blender that whips up a region around the hole just outside the event horizon where the space time is, figurative speaking, "spinning around" the black hole. This is called the ergosphere. If you drop an object so that it falls into the ergosphere on an orbit in the same direction the egrosphere is spinning, and if at the bottom the object launches part of itself backwards (like the impulsive burn of a rocket, say, shooting out propellant for thrust) so that the ejected material falls past the event horizon, the extra kick at low gravitational potential will send the remainder of the object zipping back out faster than it came in. If you do this right, it adds more kinetic energy to the ejected object than the mass energy of the stuff that was dropped in![18] This extra energy comes from the rotational energy of the black hole. You can then spin the black hole back up again by throwing stuff in off-center so that it gains angular momentum.
Warp batteries
But what if you don't have a spinning black hole? If you are an arbitrarily advanced society with the ability to manipulate mass and energy on a scale well beyond our own, you might build a rapidly rotating shell of ultra-dense material that doesn't quite form an event horizon. This could still produce the Penrose effect, allowing you to take energy from the rotational energy of the shell[19].
Material limits
Most things that store energy rely on the chemical bonds between atoms to either actively shuffle the electrons around, provide heat through chemical reactions that is fed into a heat engine, or to simply hold the energized structure together. The first two of these are generally well appreciated – a battery or fuel is no better than the ability of its chemical reactions to supply energy. The stresses imposed on the materials by the energy circulating inside the device is often less considered, but poses the ultimate limit for many of the devices described here. Consequently, to get the highest specific energy you want to use the highest possible specific strength (strength-to-weight ratio) material for making the storage device. This can be found by dividing the yield strength (in Pa) by the density (in kg/m3). The best performing steels (maraging steels) can get you around 0.2 to 0.3 MJ/kg. Kevlar is around 2.5 MJ/kg. Carbon fiber can reach 2.5 to 4 MJ/kg, depending on type, with some recent samples promising 6 to 7 MJ/kg. Despite their high strength, materials such as UHMWPE and spider silk are prone to plastic deformation and creep at high stresses and are thus not really suitable. And remember that if you run your energy storage device right up to the limits of its material strength, it will be on the verge of failure – a very explosive failure. So be sure to incorporate an adequate safety margin into your design.
To get around the limits of the chemical bond, you will need to go to energy storage methods that rely on different kinds of reactions such as nuclear or matter-antimatter reactions. These will not be constrained by the energy they can store by material strength. They will, however, be limited in the rate at which they can extract that energy by material constraints – confining the high pressure steam generated by the heat of a nuclear reactor, resisting the centrifugal forces of a spinning turbine driven by that steam, confining the magnetic fields of a magnetohydrodynamic generator or magnetic nozzle; all these require strong materials to hold the machinery together. The obvious exception is for explosives, where there is nothing confining the energy. But if you try to contain the explosion and use it to generate useful work, you are back to material strength limits again.
Carbon super-materials
The ultimate limit for materials held together by chemical bonds is the carbon-carbon bond found in things like atomically perfect graphene or carbon nanotubes (the boron-nitrogen bond offers similar strength). In principle, these could reach 45 to 120 MJ/kg if they could be made defect free (or in configurations that are resistant to crack propagation because there will inevitably be defects) and in bulk samples. In practice, realizing this promise will be very challenging – it might turn out to not be possible. But it might also be something that could be achieved by a highly advanced society, and if you want super-strong materials and compact energy storage for your setting these materials might be the sort of technology assumptions that let you do that.
Simulations of atomically perfect single walled carbon nanotubes (SWCNTs) indicate elastic stretching up to a tensile stress of approximately 80 GPa and around 9% elongation strain[20]. The nanotube behavior after this point depends on its configuration, which depends on the way its 6-carbon rings connect up with each other when winding around the tube. In the so-called zigzag configuration, SWCNTs are predicted to be brittle and fracture at about 110 GPa and a strain of 0.16. The so called armchair and chiral(5,3) configurations, on the other hand, experienced ductile deformation well beyond the elastic limit with the armchair configuration surviving in some form at up to a tensile stress of 200 GPa and a relative elongation of 0.33. The presence of defects did not significantly affect the behavior in the elastic region, but could decrease the strength of the tubes in the plastic region.
Using a density of 1.7 g/cm³, this means that an energy storage device limited by the tensile strength of carbon nanotubes could store up to about 45 MJ/kg if you limit the deformation to the elastic region. Keeping the stress at or under under the elastic 80 GPa limit is useful for two reasons. First, it provides an important safety buffer – if the structure exceeds that limit it will plastically deform rather than catastrophically failing. Second, it means that you can charge the storage system up, use the energy, and then charge it back up again. Once the system has plastically deformed it will not go back to its original shape and its ability to store energy in future cycles will be compromised.
However, if you only care about charging up the energy storage system once, ever, you can store more energy in it. Taking it all the way up to the failure stress of 200 GPa for perfect armchair nanotubes could, in principle, allow you to store close to 120 MJ/kg for tension-limited devices like flywheels or SMES. This could be promising for charging up advanced energy storage systems for use as explosives; at 120 MJ/kg your energy storage device has approximately 28 times more energy than an equal mass of TNT, and its sudden failure and release of that energy would thus provide an explosive yield roughly equivalent to the detonation of 28 times its mass of that high explosive. The ability of any real material to ever reach this limit is questionable. Even if such a material existed storing this much energy in it would put it at the limit of failure, such that slight bumps or changes in temperature could cause an explosion. Nonetheless, it is useful to science fiction authors as an upper limit to the amount of energy (explosive or otherwise) that can be stored in a device held together by chemical bonds.
When considering carbon nanotube yarns as spring energy storage, the stress and strain limits give an energy of about 2 MJ/kg (from ½ × stress at elastic limit × strain at elastic limit / density). Unlike other energy storage methods such as flywheels or SMES, charging the system up beyond its elastic limit offers no benefit – you need to put in more energy to deform it to those levels, but the relaxation back to its new equilibrium deformed shape only gives you back about the amount of energy that can be stored elastically.
Other carbon supermaterials are also possible. Nanotubes are rolled up graphene sheets whose edges are joined to make a cylinder. This suggests that graphene would have similar elastic behavior to carbon nanotubes and plastic or brittle behavior beyond that point that depends on its orientation. And thus, re-usable energy storage made with graphene sheets would likely have similar constraints on its specific energy. Simulations support this, with stress-strain curves not strongly different from that of carbon nanotubes[21]. However, large sheets of graphene are more prone to brittle fracture, as they don't have the convenient limits of being confined to a tube to limit crack propagation.
Diamond is another form of carbon, with a very different bond arrangement, that is known for its extreme strength. Diamond nanowhiskers with the [100] crystal orientation were measured to elastically stretch to an elongation strain of 0.134 with a tensile stress of 125 GPa before breaking; the theoretical maximum stress is estimated at 225 GPa with an elongation of about 0.4 but the theoretical elastic behavior does not seem to exceed the experimental values of 125 GPa and 0.134 elongation[22]. With a density of 3.52 g/cm³, this corresponds to 35 MJ/kg for diamond-backed tension supported energy storage and 2.4 MJ/kg for diamond springs, although with little margin for error in the event of failure. If you could somehow engineer diamond whiskers that could reach the theoretical maximum, then one-use tensile-limited diamond-backed energy storage systems could conceivably reach nearly 65 MJ/kg, although this device would likely be sensitive, unstable, and prone to unpredictable explosion.
Converting between energy types
Often, you have energy stored in some form and you need to use it in a different form. For example, if you are storing the energy for your laser gun in a flywheel, the mechanical energy that the flywheel puts out won't do you any good unless you can turn it into electrical energy to pump your laser. The mass and cost of the converters can be a significant factor in your design considerations – if you have an ultra-compact source of energy but need a big bulky motor to make use of it, it starts to look less attractive than one that gives you energy in the same form you need.
Electric to mechanical and back – motors and generators
An electric motor takes electrical energy and transforms it into mechanical energy. When you mechanically spin the shaft it becomes a generator, taking mechanical energy and turning it into electrical energy. Note that these are the same machine – any electric motor can be run backwards as a generator and vice versa. With modern (2021) tech, electric motors generally have an efficiency of 90 to 95%, with 99% efficiencies reported for experimental superconducting designs. Most modern electric motors have specific energies in the 1 to 2 kW/kg range, with a few that have been engineered to hell and back for ultra-high performance bleeding edge mass reduction to just barely break past 15 kW/kg[23].
Explosively pumped flux compression generator
While there are many different kinds of electric motors and generators, one kind stands out as being particularly unusual and unique with a specific application that cannot easily be met by anything else. This is the explosively pumped flux compression generator (FCG), which is technically a combination of heat engine and electric motor in one. There are different configurations, but a typical FCG operates as follows: A cylinder of high explosive is surrounded by a sheet of copper. This tube is wound with a solenoid electromagnet and energized with a pulse of electric current supplied by a capacitor bank. The explosive is then detonated on one end, producing a detonation wave that sweeps down the cylinder. As the detonation wave passes, it pushes the copper sheath outward, confining the magnetic flux from the electromagnet into a smaller and smaller area. This induces an increase in electrical current in the electromagnet, ultimately delivering much more energy than was initially input by the capacitor bank discharge[24]. As you might imagine, detonating a large quantity of high explosive inside of it (or, in some designs, surrounding it as a sleeve or jacket) is hard on the generator – these are single-use only devices, being exploded with each use. Their main application is to provide very high pulses of power, taking the substantial portion of the energy of detonation that is produced by the explosive on the order of a millisecond and turning it into a pulse of electrical energy with the same duration. Reported efficiencies for FCGs tend to run around 10% to 20%[25][26] Specific energies reported have been on the order of a few kJ/kg[27][28], with specific powers on the order of several MW/kg.
There have been proposals for flux compression generators that do not require explosives, and which could thus be reused. Such as driving a FCG with a gasoline piston[29]. This is described as an inverse railgun, using the piston stroke to move an armature up the rails in opposition to the imposed force by the current, thus generating work. In principle, any electromagnetic launcher, such as the various types of coilguns, could similarly be used in reverse. This gets to the idea that electromagnetic launchers are really rotary electric motors that have been unrolled into a linear electric motor; and running any electric motor backward gets you a generator.
Chemical to mechanical and thermal to mechanical – Heat engines
Technically, a heat engine is any device that takes in energy and entropy at high temperature and exhausts the entropy along with a certain portion of the energy at lower temperature and uses the rest of the energy to do work. This definition technically includes things like photovoltaic solar panels (which take in energy and entropy from the 6000 kelvin hot sun and exhaust the entropy at the 300 kelvin ambient temperature typical of Earth and produce electrical work in the process). But usually when people think of a heat engine, they imagine a device that takes hot gases from combustion or other processes (such as a nuclear reactor), runs those gases through various expansion, compression, and heat exchange cycles, uses these cycles to extract mechanical work, and then exhausts the entropy as a lower temperature gas. These run from the earliest Watt steam engines all the way to modern jet turbines and combined cycle steam turbines at power plants.
Internal combustion piston engines
These are the machines that power our cars. They include both gasoline engines and Diesel engines. For the latter half of the 20th century, they generally ran about 20% efficient at turning heat energy into work, with the occasional commercial design topping 25% when they wanted to advertise fuel efficiency. Fuel efficiency regulations in the early 21st century driven by climate worries drove the efficiencies up to around 30% or 35% with some advanced models achieving 50% efficiency. [30] Specific powers of modern (2021) piston engines tend to run at about 1 to 2 kW/kg, with very high performance turbocharged or supercharged models approaching 10 kW/kg. High performance piston engines can maintain these specific powers down to at least somewhat less than 100 kg of mass. [31]
Stirling piston engines
Stirling cycle engines are closed-cycle engines that re-use the same working fluid over and over again. They take in heat from an external source (such as concentrated solar, burning a fuel, or from radioactive decay), couple it to the working fluid with a heat exchanger, and use that to drive the piston cycles that generate mechanical power. Compared to internal combustion engines, Stirling engines tend to have a lower specific power and higher specific cost, but require less maintenance and can run on any available source of heat rather than only highly refined fuels. For combustion engines or other heat sources providing a similar high input temperature, the efficiencies of a Stirling engine are similar to those of an internal combustion engine.
Turbines
Turbines use a flow of fluid past a radial array of fan blades to spin a shaft; that shaft can be used for mechanical power or to drive an electrical generator. If you are looking for a turbine engine for power rather than just as a propulsive jet, you get a turboshaft engine (or, if you are using the mechanical energy to drive a propeller, a turboprop). These usually burn a liquid hydrocarbon to generate heat and pressure, and the hot, high pressure gas spins the turbine as it squirts out. They can, however, also be designed to burn gaseous hydrocarbons, hydrogen, or other fuels. Turbines take some time to spin up to full speed, and are not very efficient when not working near their optimal spin rate, so they are best for applications that require a constant power. In addition, they spin really fast but at low torque, so you will usually need a gearbox to trade speed for torque. Compared to piston engines, they are more expensive and ill-suited to applications requiring rapidly changing loads or variable power (like automotive engines) but are lower maintenance, lower vibration, can burn less volatile (and thus safer) fuels, and generally have a much higher specific energy – usually in the 5 to 12 kW/kg range. Typical designs for helicopter or maritime powerplants run at about 30 to 40% efficiency at extracting mechanical energy from the thermal energy of combustion [32] [33]. Unfortunately, turbines don't scale down very well. Below many hundreds of kilowatts, they start to lose efficiency and specific power.
A non-gaseous source of heat (like a nuclear reaction, or sunlight) can be used to boil water. The high pressure steam can then spin a turbine to generate power.
The most efficient turbines are combined cycle turbines, where the output heat from a gas turbine can be used to generate steam to run a steam turbine. These can reach efficiencies in the 60% range, and are often used for large, stationary applications like grid-scale power.
Chemical to electrical – fuel cells
A fuel cell directly extracts an electrical current from a chemical reaction. It is typically run somewhat like a battery with the fuel diffusing through an electrolyte between an anode and a cathode, and the extra electrons required to make the reaction work drive the electric current. Almost all modern (2021) fuel cells use take hydrogen as fuel and react it with atmospheric oxygen, or perhaps stored oxygen from a separate tank. Fuel cells are generally between 40 and 60% efficient. There are many different kinds of fuel cell. Some kinds only work at elevated temperatures (although they can use the heat produced by the reaction to help maintain those temperatures once they are operational). The anode of most modern (2021) fuel cells require platinum as a catalyst to break up the fuel, which is not only expensive but can cause problems when not using hydrogen as a fuel source because the platinum catalyst can get clogged up with carbon monoxide and stop working. Because they have no working parts, fuel cells are very reliable and low maintenance. Fuel cells for automotive use generally deliver about 1 to 2 kW/kg specific power.
Electrical to chemical – electrolysis
You can run a battery in reverse. By putting a voltage across a pair of electrodes in an electrolyte, you can separate out dissolved ions and other chemical species. This is called electrolysis. Electrolysis is vital for producing many metals – for example, all commercial aluminum is made by electrolysis of the aluminum oxide ore. Rechargeable batteries are essentially using an electrolysis process, and the aluminum electrolysis method has even been suggested for energy storage by running aluminum metal plates as an aluminum-air battery to create electricity.
For energy storage, the most significant electrolytic reaction is the electrolysis of water to form hydrogen and oxygen. The hydrogen is then stored for later use. As of the time of this writing (2022), this process is not price competitive with steam reforming of methane – reacting methane with water at high temperatures to form hydrogen and carbon monoxide. However, electrolysis does not release greenhouse gases into the atmosphere, while steam reforming does. This establishes a market for electrolyzed hydrogen despite its higher price, and incentivizes research into cheaper methods of water electrolysis.
It is even possible to run some kinds of fuel cells in reverse, to electrolyze water and fill up your hydrogen tanks with electricity from the grid so that you could use, for example a fuel cell car without needing to stop at a hydrogen fuel station for a refill.
Thermal to chemical
High temperatures can be used to drive chemical reactions. This has been used since the dawn of human history to cook food and provide light, warmth, and security from fire-adverse predators at our camps. It can also be used to create chemicals for energy storage. The most extensive such operation in the modern world is petroleum refining. Crude oil is heated in fractionation columns in the presence of a catalyst (a molecule or surface that allows a chemical reaction to proceed faster than it ordinarily would). This splits up the oil into hydrocarbon chains of different lengths, which are distilled out to form different grades and types of fuel. This produces gasoline (which is further separated by its octane rating), Diesel fuel, and kerosene.
Another method of using heat to store energy as chemicals is the steam reforming of methane (natural gas) to form syngas – a mix of hydrogen and carbon monoxide. While syngas is often used as a starting point for further chemical chemical reactions to make other products (such as methanol, or even artificial gasoline or Diesel fuel), it can also be burned directly for heat or the hydrogen can be separated out and used to power fuel cells.
Very high temperatures can simply be used to directly crack apart water molecules into oxygen and hydrogen. This has been suggested as a use for advanced high temperature nuclear reactors, although the author is not aware of any currently (2022) operating.
Mechanical to mechanical – drivetrains
Usually, the mechanical energy you are getting out of your energy source isn't quite what you need for your application. Maybe it has the wrong RPM or the wrong torque. Or maybe it is in the wrong place or you need to be able to idle the engine or something. So just about any source of mechanical energy being used for a mechanical application will need a collection of gearboxes, transmissions, differentials, clutches, and driveshafts. This can be minimal, like for turboprops, or extensive, like for automobiles. Drivetrains will introduce an additional source of efficiency loss - you might expect only about 80% to 90% of the input power of an automotive engine to reach the wheels, for example (depending on many details, such as type of transmission, front-wheel vs. rear wheel drive, and so on). [34] [35]
Electrical to electrical – rectifiers, inverters, and transformers
Sometimes, the electrical energy you get from your power source doesn't have the right voltage, current, or frequency that you need for your application. An inverter takes direct current (DC) and turns it into alternating current (AC). A transformer takes AC power and changes its voltage, with a reciprocal change to the current (for example, a step-up transformer might increase the voltage by a factor of 6 but decrease the current to 1/6 of it's input value). A rectifier takes AC electricity and gives you DC electricity back out. Using these tools, you can convert your electricity from the kind you get to the kind you need. However, depending on the application, you may need additional massaging of your electricity. To change the wave form, for example, or shape high energy pulses, to what is required.
Credit
Author: Luke Campbell
References
- ↑ Alissa Greenberg, "How iron-air batteries could fill gaps in renewable energy", Nova, August 23 2023
- ↑ Prachi Patel, " NASA Battery Tech to Deliver for the Grid: A battery built for satellites brings grid-scale storage down to Earth", IEEE Spectrum, 24 Sep 2023
- ↑ F. MacDougall et al., "High Energy Density Capacitors for Pulsed Power Applications"
- ↑ Hyperphysics - Energy in an Inductor
- ↑ Mustafa E. Amiryar and Keith R. Pullen, "A Review of Flywheel Energy Storage System Technologies and Their Applications", Appl. Sci. 2017, 7, 286; doi:10.3390/app7030286
- ↑ 6.0 6.1 [1] W. A. Walls and M. Driga, "Topologies for compact compensated pulsed alternators," IEEE Conference Record - Abstracts. PPPS-2001 Pulsed Power Plasma Science 2001. 28th IEEE International Conference on Plasma Science and 13th IEEE International Pulsed Power Conference (Cat. No.01CH37, Las Vegas, NV, USA, 2001, pp. 249-, doi: 10.1109/PPPS.2001.960872.
- ↑ 7.0 7.1 [2] J. H. Gully, "Power Supply Technology for Electric Guns", Presented at the Fifth EML Conference, Destin, FL, April 2 to 5, 1990. Publication No. PR-108, Center for Electromechanics, The University of Texas and Austin, Balcones Research Center
- ↑ Federico Rossi, Beatrice Castellani, and Andrea Nicolini, "Benefits and challenges of mechanical spring systems for energy storage applications", Energy Procedia 82 (2015) 805 – 810
- ↑ "Small springs could provide big power", David L. Chandler, MIT News Office, September 21, 2009
- ↑ https://www.wiley-vch.de/books/sample/3527322736_c01.pdf Manfred Klell, "Handbook of Hydrogen Storage" Edited by Michael Hirscher, chapter 1 "Storage of Hydrogen in the Pure Form" Copyright Ó 2010 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim, ISBN: 978-3-527-32273-2
- ↑ NASA: Kilopower
- ↑ Brumfiel, Geoff (May 6, 2004). "Physics: The waiting game". Nature. 429 (6987): 10–11. Bibcode:2004Natur.429...10B. doi:10.1038/429010a. PMID 15129249. S2CID 4425841.
- ↑ Harry J. Lipkin, "MONOPONUCLEOSIS - The wonderful things that monopoles can do to nuclei if they are there", ANL-HEP-CP--83-45, Presented at the "Monopole '83" Conference, University of Michigan, Ann Arbor, Michigan, October 6-9, 1983.
- ↑ 14.0 14.1 Dr. Gerald P. Jackson, "Antimatter-Based Propulsion for Exoplanet Exploration"
- ↑ Hiroshi Takahaahi and Janes Powell, "Large amounts of antiproton production by heavy ion collision", BNL 40574
- ↑ James Bickford, "Extraction of antiparticles concentrated in planetary magnetic fields"
- ↑ C. Patrignani et al. (Particle Data Group), "Magnetic Monopoles", Chin. Phys. C, 40, 100001 (2016) and 2017 update, December 1, 2017
- ↑ Jeremy D. Schnittman, "The Collisional Penrose Process", NASA GSFC
- ↑ Alexey Bobrick, Gianni Martire, "Introducing Physical Warp Drives", arXiv:2102.06824v1 [gr-qc] 12 Feb 2021
- ↑ Keka Talukdar and Apurba Krishna Mitra, "Molecular Dynamics Simulation Study on the Mechanical Properties and Fracture Behavior of Single-Wall Carbon Nanotubes" From the Edited Volume "Carbon Nanotubes - Synthesis, Characterization, Applications" Edited by Siva Yellampalli, SRM University, India
- ↑ Fan, Na & Ren, Zhenzhou & Jing, Guangyin & Guo, Jian & Peng, Bei & Jiang, Hai. (2017). "Numerical Investigation of the Fracture Mechanism of Defective Graphene Sheets." Materials 10(2):164. DOI:10.3390/ma10020164.
- ↑ Nie, A., Bu, Y., Li, P. et al. Approaching diamond’s theoretical elasticity and strength limits. Nat Commun 10, 5533 (2019).
- ↑ NASA Tests Machine to Power the Future of Aviation Propulsion (Aug 11, 2021)
- ↑ Andreas A. Neuber and James C. Dickens, "Magnetic Flux Compression Generators", Proceedings of the IEEE, Vol 92 No. 7, Pg. 1205 - 1215 (2004) 10.1109/JPROC.2004.829001.
- ↑ C. M. Fowler, R. S. Caird, and W. B. Garn, "An Introduction to Explsoive Magnetic Flux Compression Generators" Los Alamos National Laboratory report LA-5890-MS (1975)
- ↑ C. M. Fowler and L. L. Altgilbers, "Magnetic Flux Compression Generators: a Tutorial and Survey"
- ↑ Q. Sun, C. Sun, X. Gong, W. Xie, Z. Liu, W. Dai, Y. Chi, and S. Fu, ”An Effective Explosive Magnetic Flux Compression Generator with 102 nH Inductance Load”, Preprint, Megagauss IX Conference, Russia (2002).
- ↑ Patrik Appelgren, "Gigawatt Pulsed Power Technologies and Applications", Doctoral Thesis, School of Electrical Engineering, Space and Plasma Physics, Royal Institute of Technology, Stockholm, Sweden 2011
- ↑ R. Marshall, "A reusable inverse railgun magnetic flux compression generator to suit the earth-to-space-rail-launcher," in IEEE Transactions on Magnetics, vol. 20, no. 2, pp. 223-226, March 1984, doi: 10.1109/TMAG.1984.1063049.
- ↑ Mercedes AMG F1 engine achieves 50 percent thermal efficiency
- ↑ 10 Years of BMW F1 Engines
- ↑ GE Turbines and small Engines Overview
- ↑ Comparison of Helicopter Turboshaft Engines
- ↑ Where’d My Horsepower Go? Drivetrain Power Loss & The 15% "Rule"
- ↑ Drivetrain losses (efficiency)