Superconductive Magnetic Energy Storage
Inductors, like capacitors, are electrical components that can directly store electrical energy and discharge it quickly[1]. An inductor is made by flowing electrical current and the reluctance of the magnetic field that current creates to change its strength. When you try to change a magnetic field, you get the production of an electric field that acts to drive currents in the direction that would maintain the field. This "magnetic inertia" is called inductance. If you have a device with a large inductance, interrupting the flow of current will start to decrease the stored magnetic field resulting in a "backlash" as the field resists the changes and creates a large voltage to ram more current through to maintain itself. In this way, you can consider the magnetic field itself to be storing the energy and it is often most convenient to consider it in this way when doing the physics.
Usually, inductors are made in the form of solenoids - a coil of wire wound in a tube shape. The problem, of course, is that in normal materials electrical resistance will almost immediately drain away all your energy in the form of heat. You might be able to use large inductors to build up energy over a fraction of a second from a more slowly discharging power source and then suddenly switch it all at once to ram that electricity through your device at very high power. But for any long term energy storage with inductors you will need to use those exotic materials called superconductors.
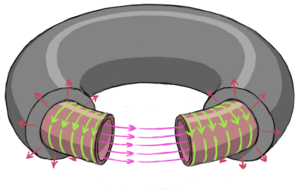
Superconductors allow the flow of electricity through them without any resistance at all. In this way, a superconductive solenoid can be used for Superconductive Magnetic Energy Storage (SMES). To limit the exposure of the environment to the extreme magnetic fields created, the solenoid tube is usually bent around so the ends connect, making a shape like a bagel or doughnut called a torus. Once charged up, the supercurrent flows endlessly around surface of the torus creating a very high magnetic field that is confined entirely to the inside of the torus tube. Without this bending, anyone near one of these SMES would be in danger of being punctured by flying ferromagnetic metal objects or suffering from inductive currents zapping their body if they moved past too fast.
There are several limits on SMES's ability to store energy. The first is that all known superconductors can only remain superconductive at cryogenic temperatures, generally requiring liquid nitrogen or liquid helium to work. Room temperature and pressure superconductors may be possible, but we haven't discovered any yet and it is also possible that none may exist at all. If a superconductor's temperature exceeds this critical temperature, it quenches, or becomes non-superconductive. The sudden resistive heating from all the SMES energy being driven through the quenched superconductor can cause arcing, vaporization, and explosions.
Second, superconductors only remain superconducting up to a critical magnetic field. This critical field depends on the temperature (and goes to zero at the critical temperature). If the field exceeds the critical field, again the superconductor will quench. This means you will want to keep the operating temperature of the SMES well below the critical temperature at which it becomes non-superconducting. The energy density of the SMES depends on the magnetic field it contains:
E / V = 0.4 × B² kJ/liter
where B is the magnetic field strength in tesla, E is the stored energy, and V is the interior volume of the torus tube.
Third, while electric currents create magnetic fields, magnetic fields in turn exert forces on electric currents. Including the electric currents that are generating them. These self forces act to push the SMES torus apart. If the structure of the SMES is not able to handle the tensile forces, it will break and explode. This is what sets the upper limit on the specific energy – the strength of the backing material wrapped around the torus tube to keep the solenoid together. The specific energy of the SMES is thus limited by the material limits of their backing.
In principle, you can discharge a SMES essentially instantly. Flip a switch to re-route the current going through it into an electrical load and all of its energy can be dumped at once. In practice, any electrical system will have some capacitance which gives a finite time to the discharge – the inductor will ram its current into the load, but the capacitance of the load will store some of that energy as charge separation that builds up to resist the inductor's push. The capacitor connected to the inductor forms an electrical device called an LC circuit (or LRC circuit, when resistance is added as well), where energy will be sloshed back and forth between the capacitor and the inductor (and bled off by the resistance). One cycle of oscillation takes a time of 2 π √[L C], where L is the inductance of the SMES and C is the capacitance of the load. So to fully discharge the SMES, it will take half of a cycle, or Δt = π √[L C]. When you add in the resistance of the load, things get a bit more complicated and you're likely going to end up with an overdamped response, but this very basic analysis still shows several things: you can have very high specific powers from a SMES, and to maximize the specific power you will want to minimize the inductance of the SMES and the capacitance of the load. Unfortunately, the amount of energy you can store is proportional to the inductance. One way to get the best of both worlds is to tap the SMES from multiple switches along its length, effectively separating the system into a number of separate inductors discharging in parallel.
An additional issue when working with large inductors is the switching problem. As soon as you start to throw a switch to divert the current from the inductor into the load, you get a small gap just as the switch is breaking the electrical connection that is interrupting the flow of current. The inductor's response is to concentrate all of the voltage it generates across this tiny gap in order to maintain its current. This generates an electrical arc, producing a low resistance path shorting the switch. As the switch continues to move apart, the arc grows so that it continues to connect the two terminals of the switch. This short circuits the whole circuit path, preventing any electricity from getting to the load. It also drops a lot of energy suddenly into the switch, likely frying the switch, ruining your SMES, and quite possibly causing an explosion. There are ways around this. For example the load might be connected to terminals shorted by a section of superconductive wire. If the wire is uniformly quenched, you end up with a sudden high resistance path across the wire and a lower resistance path through the load, and so the current is shunted through the load instead of causing an unwanted arc.
If you are confining yourself to modern tech, REBCO superconductors allow magnets with fields in the 20 to 40 tesla range, with engineers optimistic of reaching 60 tesla soon. This corresponds to energy densities of 160 kJ/liter, 640 kJ/liter, and 1.44 MJ/liter, respectively, in the field-filled region. If they are held together with the best carbon fiber backing material, they may be able achieve a specific energy of between 2 and 4 MJ/kg, with an energy density in the backing material of 3 to 8 MJ/kg. The total energy density for the combination of the backing and field region is thus in the range of 150 to 1000 kJ/liter. Switching equipment, insulation, refrigerator pumps, helium recovery systems, quench protection, and other equipment will reduce these values somewhat, but if a low mass, compact SMES was desired, performance in the range of 2 MJ/kg and 0.5 MJ/liter would be readily achievable, with 3+ MJ/kg and close to 1 MJ/liter possible with some work. Modern SMES systems will need to be kept at cryogenic temperatures. This will invariably result in some energy loss as refrigerator pumps are used to keep the superconductors cool, but with large systems this energy loss can be reasonably tolerable for many applications.
In the far future, you might imagine that room temperature superconductors have been discovered. The critical magnetic field can be expected to increase roughly in proportion to the critical temperature, so if the critical temperature is approximately 4 times higher than modern REBCO suberconductors, the energy density of the field region will be about 16 times higher. So you might have between 3 and 20 MJ/liter, going by a straight scaling of what modern superconductive magnets can (or are expected to) achieve. If the superconductor is a spin triplet superconductor, or if it has an even higher critical temperature, the field and energy density could be even higher! The ultimate limit of the specific energy will be given by the tensile strength of the backing material, which for atomically perfect graphene or hexagonal boron nitride might get you 60 or so MJ/kg. You might want to include a safety factor in this, to prevent it bursting on you if anything jostles or slightly weakens or damages it, however!
Credit
Author: Luke Campbell